# Linalg Dialect Rationale: The Case For Compiler-Friendly Custom Operations
[TOC]
## Introduction
### Positioning
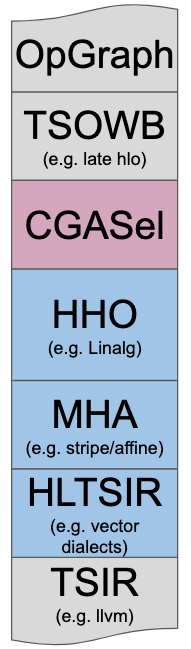 This document describes the key design principles
that led to the existing implementation of Linalg and aims at exposing
the tradeoffs involved when building higher-level Intermediate
Representations (IR) and Dialects to facilitate code
generation. Consider the simplified schema describing codegen in MLIR.
Linalg is designed to solve the High-level Hierarchical Optimization
(HHO box) and to interoperate nicely within a
*Mixture Of Expert Compilers* environment (i.e. the *CGSel* box).
This work is inspired by a wealth of [prior art](#prior_art) in
the field, from which it seeks to learn key lessons. This documentation
and introspection effort also comes in the context of the proposal for a
working group for discussing the [Development of high-level Tensor Compute
Primitives dialect(s) and
transformations](https://llvm.discourse.group/t/development-of-high-level-tensor-compute-primitives-dialect-s-and-transformations/388/3).
We hope that the lessons from prior art, the design principles outlined in
this doc and the architecture of Linalg can help inform the community on a
path to defining these High-Level Tensor Compute Primitives.
### Inception
Linalg started as a pragmatic dialect to bootstrap code generation in MLIR, by
*defining away* complex code generation problems like precise dependence
analysis or polyhedral code generation and by introducing the ability to call
into fast library implementations when available. Linalg **defines ops and
transformations declaratively** and was originally restricted to ops with
*linear-algebra like* semantics (`pointwise`, `matmul`, `conv`...). This
approach enables building a high-level productivity-first codegen solution that
leverages *both* compiler optimizations *and* efficient library implementations
so as not to miss out on simple performance benefits. For example, if
one's favorite HPC library or ISA has a `matmul` primitive running at 95% of
the achievable peak performance, for operands stored in some memory, one should
be able to **use the primitive** when possible *and* generate code otherwise.
However, as the design of Linalg co-evolved with the design of MLIR, it became
apparent that it could extend to larger application domains than just machine
learning on dense tensors.
The design and evolution of Linalg follow a *codegen-friendly* approach where
the IR and the transformations evolve hand-in-hand.
The key idea is that op semantics *declare* and transport information that is
traditionally obtained by compiler analyses.
This information captures the legality and applicability of transformations and
is **not lost by lowering prematurely to loop or CFG form**. The key
transformations are designed so as to **preserve this information** as long as
necessary. For example, `linalg.matmul` remains `linalg.matmul` after tiling
and fusion.
Furthermore, Linalg decouples transformation validity from profitability
considerations and voluntarily leaves the latter aside in the first iteration
(see the [suitability for search](#suitability_for_search) guiding principle).
The first incarnation of these ideas was presented as an example at the
EuroLLVM 2019 developer's meeting as part of the
[Linalg section](https://llvm.org/devmtg/2019-04/slides/Tutorial-AminiVasilacheZinenko-MLIR.pdf)
of the first [MLIR Tutorial](https://www.youtube.com/watch?v=cyICUIZ56wQ).
### Evolution
Since the initial implementation, the design has evolved with, and partially
driven the evolution of the core MLIR infrastructure to use
[Regions](https://mlir.llvm.org/docs/LangRef/#regions),
[OpInterfaces](https://mlir.llvm.org/docs/Interfaces/),
[ODS](https://mlir.llvm.org/docs/OpDefinitions/) and
[Declarative Rewrite Rules](https://mlir.llvm.org/docs/DeclarativeRewrites/)
among others. The approach adopted by Linalg was extended to become
[StructuredOps abstractions](
https://drive.google.com/drive/u/0/folders/1sRAsgsd8Bvpm_IxREmZf2agsGU2KvrK-),
with Linalg becoming its incarnation on tensors and buffers.
It is complemented by the
[Vector dialect](https://mlir.llvm.org/docs/Dialects/Vector/),
which defines structured operations on vectors, following the same rationale and
design principles as Linalg. (Vector dialect includes the higher-level
operations on multi-dimensional vectors and abstracts away the lowering to
single-dimensional vectors).
The Linalg dialect itself grew beyond linear algebra-like operations to become
more expressive, in particular by providing an abstraction of a loop nest
supporting parallelism, reductions and sliding windows around arbitrary MLIR
[regions](https://mlir.llvm.org/docs/LangRef/#regions). It also has the
potential of growing beyond *dense* linear-algebra to support richer data
types, such as sparse and ragged tensors and buffers.
Linalg design remains open to evolution and cross-pollination with other
dialects and approaches. It has been successfully used as the staging ground
for code generation-related abstractions, spinning off the generalization of
the following:
- the `!linalg.view` type folded into the *"Strided MemRef"* type while
preserving structure to allow calling into external C++ libraries with
unsurprising ABI conventions;
- the `linalg.view` and `linalg.subview` ops evolved into the standard dialect;
- the `linalg.for`, `linalg.load` and `linalg.store` ops evolved into a prelude
to the *structured control flow* dialect (named `LoopOps`).
More components can be extracted, redesigned and generalized when new uses or
requirements arise.
Several [design questions](#open_issues) remain open in Linalg, which does not
claim to be a general solution to all compilation problems.
It does aim at driving thinking and implementations of domain-specific
abstractions where programmer's intent can be captured at a very high level,
directly in the IR.
Given the evolution of the scope, it becomes apparent that a better name than
"Linalg" could remove some of the confusions related to the dialect (and the
underlying approach), its goals and limitations.
## Prior Art
Linalg draws inspiration from decades of prior art to design a modern a
pragmatic solution. The following non-exhaustive list refers to some of the
projects that influenced Linalg design:
- [ONNX](https://onnx.ai/),
- [LIFT](https://www.lift-project.org/),
- [XLA](https://www.tensorflow.org/xla/architecture),
- [Halide](https://halide-lang.org/) and [TVM](https://tvm.apache.org/),
- [TACO](http://tensor-compiler.org/),
- [Darkroom](http://darkroom-lang.org/) and [Terra](http://terralang.org/),
- [Sigma-LL](http://spiral.ece.cmu.edu:8080/pub-spiral/pubfile/cgo16-preprint_248.pdf),
- [Tensor Comprehensions](https://arxiv.org/abs/1802.04730),
- [Polyhedral Compilers](https://en.wikipedia.org/wiki/Polytope_model),
- the [Affine dialect](https://mlir.llvm.org/docs/Dialects/Affine/) in MLIR,
- Generic Loop Transformations (see Ken Kennedy's
[Optimizing Compilers for Modern Architectures](
https://www.elsevier.com/books/optimizing-compilers-for-modern-architectures/allen/978-0-08-051324-9))
- Traditional compiler CFGs with SSA forms.
Additionally, experience with the following tools proved very valuable when
thinking holistically about how all these components interplay all the way
up to the user and down to the hardware:
- the [Torch](http://torch.ch/) machine-learning framework,
- the LLVM compiler, specifically in JIT mode,
- high-performance libraries (MKL, CUBLAS, FBFFT)
- the [PeachPy](https://www.cs.utexas.edu/users/flame/BLISRetreat/BLISRetreatTalks/PeachPy.pdf) assembler
- current and potentially upcoming hardware ISAs.
The novelty of MLIR's code base and its unprecedented support for defining and
mixing abstractions, enabling one to reflect on and integrate the key elements
of the prior art success as well as avoid the common pitfalls in the area of
code generation. Thus, instead of diverging into a discussion about the
implications of adopting any of the existing solutions, Linalg had the
possibility to build on all of them and learn from their experience while
leveraging the benefit of hindsight.
The following reflections on prior art have influenced the design of Linalg.
The discussion is by no means exhaustive but should capture the key motivations
behind Linalg.
### Lessons from ONNX
ONNX is a specification of operations that appear in Machine Learning
workloads. As such, it is predominantly driven by the expressiveness requirements
of ML, and less by the considerations of IR design for HPC code generation.
Similarly to ONNX, Linalg defines *"semantically charged" named ops*.
But it also considers *transformations on these ops* as a key component and
defines the IR to support the transformations, preferring transformations over
expressiveness if necessary.
Linalg hopes to additionally address the following:
- facilitate frontend-compiler co-design by taking into account compiler
transformations and lowerings in op definition;
- minimize the set of available ops by making them non-overlapping with each
other, thus simplifying the intermediate representation.
### Lessons from LIFT
[LIFT](https://www.lift-project.org/) is a system to write computational
kernels based on functional abstractions. Transformations are
represented by additional nodes in the IR, whose semantics are at the
level of the algorithm (e.g. `partialReduce`).
LIFT applies and composes transformations by using [local rewrite
rules](https://www.lift-project.org/presentations/2015/ICFP-2015.pdf) that
embed these additional nodes directly in the functional abstraction.
Similarly to LIFT, Linalg uses local rewrite rules implemented with the MLIR
[Declarative Rewrite Rules](https://mlir.llvm.org/docs/DeclarativeRewrites/)
mechanisms.
Linalg builds on, and helps separate concerns in the LIFT approach as follows:
- transformations are either separated from the representation or expressed as
composable attributes that are independent of the actual computation,
avoiding intricate effects on performance;
- abstractions are split into smaller components (e.g., control flow and data
structure abstractions) potentially reusable across different dialects in the
MLIR's open ecosystem.
LIFT is expected to further influence the design of Linalg as it evolves. In
particular, extending the data structure abstractions to support non-dense
tensors can use the experience of LIFT abstractions for
[sparse](https://www.lift-project.org/publications/2016/harries16sparse.pdf)
and [position-dependent
arrays](https://www.lift-project.org/publications/2019/pizzuti19positiondependentarrays.pdf).
### Lessons from XLA
[XLA](https://www.tensorflow.org/xla/architecture) is one of the first
post-Theano ML compilers that was introduced as a pragmatic compilation
solution for TensorFlow. It shines on Google's xPU
hardware and is an important piece of the puzzle. It is particularly good at
(1) transforming code back and forth between the scalar and the vector
worlds, (2) passing function boundaries for handling both host and device
code, and (3) complying to stringent requirements imposed by energy-efficient
xPUs.
XLA followed a pragmatic design process where the compiler is given perfect
knowledge of each op's semantic, all starting from the mighty `conv` and
`matmul` ops. XLA transformations consist of writing emitters that compose, as C++
functions. Perfect op semantics knowledge has 2 big benefits: (1) transformations are
correct by construction (2) very strong performance on difficult xPU targets.
Similarly, Linalg ops *"know their semantics"* and *"know how to transform and
lower themselves"*. The means by which this information is made available and
how it is used in MLIR are, however, very different.
Linalg hopes to additionally address the following:
- HLOs are expressive as a whole, but each op has very limited and fixed
semantics: ops are not configurable. As a consequence, HLOs have evolved into
a too large set of ops whose semantics intersect.
This echoes the ops proliferation problem also exhibited by ONNX.
- Reliance on perfect op knowledge leads to situations where transformations and
ops end up needing to know about each other's semantics (e.g. during fusion).
Since the transformations themselves are not simple local rewrite patterns
(unlike LIFT), code complexity grows quickly.
- XLA lacks an independent IR that can be inspected, unit tested and used
independently. This monolithic design makes the system not portable: xPU passes
and GPU passes do not share much code.
### Lessons from Halide and TVM
[Halide](https://halide-lang.org/) is a DSL embedded in C++ that provides a
way of metaprogramming the HalideIR and applying transformations declaratively
to let the expert user transform and optimize the program in tailored ways.
Halide, initially targeted the SIGGRAPH community but is now more generally
applicable. [TVM](https://tvm.apache.org/) is an evolution of Halide into the
machine learning and deep-neural network space, based on HalideIR.
The Halide transformation methodology follows similar principles to the
[URUK](http://icps.u-strasbg.fr/~bastoul/research/papers/GVBCPST06-IJPP.pdf)
and
[CHiLL](https://pdfs.semanticscholar.org/6a46/20589f63f3385707d2d590f7b7dc8ee4d74f.pdf)
compiler transformation frameworks, but without the strengths (and especially
complexity) of the polyhedral model.
Halide particularly shines at making the HPC transformation methodology
accessible to $\Omega$(10-100) users, at a time when polyhedral tools are
still only accessible to $\Omega$(1-10) users. Halide makes heavy usage of
canonicalization rules that are also very prevalent in MLIR.
Linalg hopes to additionally address the following:
- Halide scheduling is powerful and explores a large swath of possible
transformations. But it's still too hard for newcomers to use or extend. The
level of performance you get from Halide is very different depending on
whether one is a seasoned veteran or a newcomer. This is especially true as
the number of transformations grows.
- Halide raises rather than lowers in two ways, going counter-current to the
design goals we set for high-level codegen abstractions in MLIR. First,
canonical Halide front-end code uses explicit indexing and math on scalar
values, so to target BLAS/DNN libraries one needs to add pattern matching
which is similarly brittle as in the affine case. While Halide's performance
is on par with the libraries on programmable targets (CPU/GPU), that
approach doesn't work on mobile accelerators or on xPUs, where the framework
ingests whole-tensor operations.
Second, reductions and scans are expressed using serial iteration, again
requiring pattern matching before they can be transformed (e.g. to do a
reduction using atomics, or hierarchically). The lesson to draw is that we
should start with higher-level primitives than Halide.
### Lessons from Tensor Comprehensions
[Tensor Comprehensions](https://arxiv.org/abs/1802.04730) is a
high-level language to express tensor computations with a syntax
generalizing the Einstein notation, coupled to an end-to-end
compilation flow capable of lowering to efficient GPU code. It was
integrated with 2 ML frameworks: Caffe2 and PyTorch.
This document describes the key design principles
that led to the existing implementation of Linalg and aims at exposing
the tradeoffs involved when building higher-level Intermediate
Representations (IR) and Dialects to facilitate code
generation. Consider the simplified schema describing codegen in MLIR.
Linalg is designed to solve the High-level Hierarchical Optimization
(HHO box) and to interoperate nicely within a
*Mixture Of Expert Compilers* environment (i.e. the *CGSel* box).
This work is inspired by a wealth of [prior art](#prior_art) in
the field, from which it seeks to learn key lessons. This documentation
and introspection effort also comes in the context of the proposal for a
working group for discussing the [Development of high-level Tensor Compute
Primitives dialect(s) and
transformations](https://llvm.discourse.group/t/development-of-high-level-tensor-compute-primitives-dialect-s-and-transformations/388/3).
We hope that the lessons from prior art, the design principles outlined in
this doc and the architecture of Linalg can help inform the community on a
path to defining these High-Level Tensor Compute Primitives.
### Inception
Linalg started as a pragmatic dialect to bootstrap code generation in MLIR, by
*defining away* complex code generation problems like precise dependence
analysis or polyhedral code generation and by introducing the ability to call
into fast library implementations when available. Linalg **defines ops and
transformations declaratively** and was originally restricted to ops with
*linear-algebra like* semantics (`pointwise`, `matmul`, `conv`...). This
approach enables building a high-level productivity-first codegen solution that
leverages *both* compiler optimizations *and* efficient library implementations
so as not to miss out on simple performance benefits. For example, if
one's favorite HPC library or ISA has a `matmul` primitive running at 95% of
the achievable peak performance, for operands stored in some memory, one should
be able to **use the primitive** when possible *and* generate code otherwise.
However, as the design of Linalg co-evolved with the design of MLIR, it became
apparent that it could extend to larger application domains than just machine
learning on dense tensors.
The design and evolution of Linalg follow a *codegen-friendly* approach where
the IR and the transformations evolve hand-in-hand.
The key idea is that op semantics *declare* and transport information that is
traditionally obtained by compiler analyses.
This information captures the legality and applicability of transformations and
is **not lost by lowering prematurely to loop or CFG form**. The key
transformations are designed so as to **preserve this information** as long as
necessary. For example, `linalg.matmul` remains `linalg.matmul` after tiling
and fusion.
Furthermore, Linalg decouples transformation validity from profitability
considerations and voluntarily leaves the latter aside in the first iteration
(see the [suitability for search](#suitability_for_search) guiding principle).
The first incarnation of these ideas was presented as an example at the
EuroLLVM 2019 developer's meeting as part of the
[Linalg section](https://llvm.org/devmtg/2019-04/slides/Tutorial-AminiVasilacheZinenko-MLIR.pdf)
of the first [MLIR Tutorial](https://www.youtube.com/watch?v=cyICUIZ56wQ).
### Evolution
Since the initial implementation, the design has evolved with, and partially
driven the evolution of the core MLIR infrastructure to use
[Regions](https://mlir.llvm.org/docs/LangRef/#regions),
[OpInterfaces](https://mlir.llvm.org/docs/Interfaces/),
[ODS](https://mlir.llvm.org/docs/OpDefinitions/) and
[Declarative Rewrite Rules](https://mlir.llvm.org/docs/DeclarativeRewrites/)
among others. The approach adopted by Linalg was extended to become
[StructuredOps abstractions](
https://drive.google.com/drive/u/0/folders/1sRAsgsd8Bvpm_IxREmZf2agsGU2KvrK-),
with Linalg becoming its incarnation on tensors and buffers.
It is complemented by the
[Vector dialect](https://mlir.llvm.org/docs/Dialects/Vector/),
which defines structured operations on vectors, following the same rationale and
design principles as Linalg. (Vector dialect includes the higher-level
operations on multi-dimensional vectors and abstracts away the lowering to
single-dimensional vectors).
The Linalg dialect itself grew beyond linear algebra-like operations to become
more expressive, in particular by providing an abstraction of a loop nest
supporting parallelism, reductions and sliding windows around arbitrary MLIR
[regions](https://mlir.llvm.org/docs/LangRef/#regions). It also has the
potential of growing beyond *dense* linear-algebra to support richer data
types, such as sparse and ragged tensors and buffers.
Linalg design remains open to evolution and cross-pollination with other
dialects and approaches. It has been successfully used as the staging ground
for code generation-related abstractions, spinning off the generalization of
the following:
- the `!linalg.view` type folded into the *"Strided MemRef"* type while
preserving structure to allow calling into external C++ libraries with
unsurprising ABI conventions;
- the `linalg.view` and `linalg.subview` ops evolved into the standard dialect;
- the `linalg.for`, `linalg.load` and `linalg.store` ops evolved into a prelude
to the *structured control flow* dialect (named `LoopOps`).
More components can be extracted, redesigned and generalized when new uses or
requirements arise.
Several [design questions](#open_issues) remain open in Linalg, which does not
claim to be a general solution to all compilation problems.
It does aim at driving thinking and implementations of domain-specific
abstractions where programmer's intent can be captured at a very high level,
directly in the IR.
Given the evolution of the scope, it becomes apparent that a better name than
"Linalg" could remove some of the confusions related to the dialect (and the
underlying approach), its goals and limitations.
## Prior Art
Linalg draws inspiration from decades of prior art to design a modern a
pragmatic solution. The following non-exhaustive list refers to some of the
projects that influenced Linalg design:
- [ONNX](https://onnx.ai/),
- [LIFT](https://www.lift-project.org/),
- [XLA](https://www.tensorflow.org/xla/architecture),
- [Halide](https://halide-lang.org/) and [TVM](https://tvm.apache.org/),
- [TACO](http://tensor-compiler.org/),
- [Darkroom](http://darkroom-lang.org/) and [Terra](http://terralang.org/),
- [Sigma-LL](http://spiral.ece.cmu.edu:8080/pub-spiral/pubfile/cgo16-preprint_248.pdf),
- [Tensor Comprehensions](https://arxiv.org/abs/1802.04730),
- [Polyhedral Compilers](https://en.wikipedia.org/wiki/Polytope_model),
- the [Affine dialect](https://mlir.llvm.org/docs/Dialects/Affine/) in MLIR,
- Generic Loop Transformations (see Ken Kennedy's
[Optimizing Compilers for Modern Architectures](
https://www.elsevier.com/books/optimizing-compilers-for-modern-architectures/allen/978-0-08-051324-9))
- Traditional compiler CFGs with SSA forms.
Additionally, experience with the following tools proved very valuable when
thinking holistically about how all these components interplay all the way
up to the user and down to the hardware:
- the [Torch](http://torch.ch/) machine-learning framework,
- the LLVM compiler, specifically in JIT mode,
- high-performance libraries (MKL, CUBLAS, FBFFT)
- the [PeachPy](https://www.cs.utexas.edu/users/flame/BLISRetreat/BLISRetreatTalks/PeachPy.pdf) assembler
- current and potentially upcoming hardware ISAs.
The novelty of MLIR's code base and its unprecedented support for defining and
mixing abstractions, enabling one to reflect on and integrate the key elements
of the prior art success as well as avoid the common pitfalls in the area of
code generation. Thus, instead of diverging into a discussion about the
implications of adopting any of the existing solutions, Linalg had the
possibility to build on all of them and learn from their experience while
leveraging the benefit of hindsight.
The following reflections on prior art have influenced the design of Linalg.
The discussion is by no means exhaustive but should capture the key motivations
behind Linalg.
### Lessons from ONNX
ONNX is a specification of operations that appear in Machine Learning
workloads. As such, it is predominantly driven by the expressiveness requirements
of ML, and less by the considerations of IR design for HPC code generation.
Similarly to ONNX, Linalg defines *"semantically charged" named ops*.
But it also considers *transformations on these ops* as a key component and
defines the IR to support the transformations, preferring transformations over
expressiveness if necessary.
Linalg hopes to additionally address the following:
- facilitate frontend-compiler co-design by taking into account compiler
transformations and lowerings in op definition;
- minimize the set of available ops by making them non-overlapping with each
other, thus simplifying the intermediate representation.
### Lessons from LIFT
[LIFT](https://www.lift-project.org/) is a system to write computational
kernels based on functional abstractions. Transformations are
represented by additional nodes in the IR, whose semantics are at the
level of the algorithm (e.g. `partialReduce`).
LIFT applies and composes transformations by using [local rewrite
rules](https://www.lift-project.org/presentations/2015/ICFP-2015.pdf) that
embed these additional nodes directly in the functional abstraction.
Similarly to LIFT, Linalg uses local rewrite rules implemented with the MLIR
[Declarative Rewrite Rules](https://mlir.llvm.org/docs/DeclarativeRewrites/)
mechanisms.
Linalg builds on, and helps separate concerns in the LIFT approach as follows:
- transformations are either separated from the representation or expressed as
composable attributes that are independent of the actual computation,
avoiding intricate effects on performance;
- abstractions are split into smaller components (e.g., control flow and data
structure abstractions) potentially reusable across different dialects in the
MLIR's open ecosystem.
LIFT is expected to further influence the design of Linalg as it evolves. In
particular, extending the data structure abstractions to support non-dense
tensors can use the experience of LIFT abstractions for
[sparse](https://www.lift-project.org/publications/2016/harries16sparse.pdf)
and [position-dependent
arrays](https://www.lift-project.org/publications/2019/pizzuti19positiondependentarrays.pdf).
### Lessons from XLA
[XLA](https://www.tensorflow.org/xla/architecture) is one of the first
post-Theano ML compilers that was introduced as a pragmatic compilation
solution for TensorFlow. It shines on Google's xPU
hardware and is an important piece of the puzzle. It is particularly good at
(1) transforming code back and forth between the scalar and the vector
worlds, (2) passing function boundaries for handling both host and device
code, and (3) complying to stringent requirements imposed by energy-efficient
xPUs.
XLA followed a pragmatic design process where the compiler is given perfect
knowledge of each op's semantic, all starting from the mighty `conv` and
`matmul` ops. XLA transformations consist of writing emitters that compose, as C++
functions. Perfect op semantics knowledge has 2 big benefits: (1) transformations are
correct by construction (2) very strong performance on difficult xPU targets.
Similarly, Linalg ops *"know their semantics"* and *"know how to transform and
lower themselves"*. The means by which this information is made available and
how it is used in MLIR are, however, very different.
Linalg hopes to additionally address the following:
- HLOs are expressive as a whole, but each op has very limited and fixed
semantics: ops are not configurable. As a consequence, HLOs have evolved into
a too large set of ops whose semantics intersect.
This echoes the ops proliferation problem also exhibited by ONNX.
- Reliance on perfect op knowledge leads to situations where transformations and
ops end up needing to know about each other's semantics (e.g. during fusion).
Since the transformations themselves are not simple local rewrite patterns
(unlike LIFT), code complexity grows quickly.
- XLA lacks an independent IR that can be inspected, unit tested and used
independently. This monolithic design makes the system not portable: xPU passes
and GPU passes do not share much code.
### Lessons from Halide and TVM
[Halide](https://halide-lang.org/) is a DSL embedded in C++ that provides a
way of metaprogramming the HalideIR and applying transformations declaratively
to let the expert user transform and optimize the program in tailored ways.
Halide, initially targeted the SIGGRAPH community but is now more generally
applicable. [TVM](https://tvm.apache.org/) is an evolution of Halide into the
machine learning and deep-neural network space, based on HalideIR.
The Halide transformation methodology follows similar principles to the
[URUK](http://icps.u-strasbg.fr/~bastoul/research/papers/GVBCPST06-IJPP.pdf)
and
[CHiLL](https://pdfs.semanticscholar.org/6a46/20589f63f3385707d2d590f7b7dc8ee4d74f.pdf)
compiler transformation frameworks, but without the strengths (and especially
complexity) of the polyhedral model.
Halide particularly shines at making the HPC transformation methodology
accessible to $\Omega$(10-100) users, at a time when polyhedral tools are
still only accessible to $\Omega$(1-10) users. Halide makes heavy usage of
canonicalization rules that are also very prevalent in MLIR.
Linalg hopes to additionally address the following:
- Halide scheduling is powerful and explores a large swath of possible
transformations. But it's still too hard for newcomers to use or extend. The
level of performance you get from Halide is very different depending on
whether one is a seasoned veteran or a newcomer. This is especially true as
the number of transformations grows.
- Halide raises rather than lowers in two ways, going counter-current to the
design goals we set for high-level codegen abstractions in MLIR. First,
canonical Halide front-end code uses explicit indexing and math on scalar
values, so to target BLAS/DNN libraries one needs to add pattern matching
which is similarly brittle as in the affine case. While Halide's performance
is on par with the libraries on programmable targets (CPU/GPU), that
approach doesn't work on mobile accelerators or on xPUs, where the framework
ingests whole-tensor operations.
Second, reductions and scans are expressed using serial iteration, again
requiring pattern matching before they can be transformed (e.g. to do a
reduction using atomics, or hierarchically). The lesson to draw is that we
should start with higher-level primitives than Halide.
### Lessons from Tensor Comprehensions
[Tensor Comprehensions](https://arxiv.org/abs/1802.04730) is a
high-level language to express tensor computations with a syntax
generalizing the Einstein notation, coupled to an end-to-end
compilation flow capable of lowering to efficient GPU code. It was
integrated with 2 ML frameworks: Caffe2 and PyTorch.
 The compilation flow combines [Halide](#lessonshalide) and a Polyhedral Compiler
derived from [ISL](https://en.wikipedia.org/wiki/Integer_set_library)
and uses both HalideIR and the ISL *schedule-tree* IR.
The compiler provides a collection of polyhedral compilation
algorithms to perform fusion and favor multi-level parallelism and
promotion to deeper levels of the memory hierarchy.
Tensor Comprehensions showed that, fixing a few predefined strategies
with parametric transformations and tuning knobs, can already provide
great results. In that previous work, simple
genetic search combined with an autotuning framework was sufficient
to find good implementations in the ***non-compute bound regime***.
This requires code versions obtainable by the
various transformations to encompass versions that get close to the
roofline limit.
The ultimate goal of Tensor Comprehensions was to concretely mix
Halide high-level transformations with polyhedral mid-level
transformations and build a pragmatic system that could take advantage
of both styles of compilation.
Linalg hopes to additionally address the following:
- Halide was never properly used in Tensor Comprehensions beyond shape
inference. Most of the investment went into simplifying polyhedral
transformations and building a usable end-to-end system. MLIR was
deemed a better infrastructure to mix these types of compilation.
- The early gains provided by reusing established infrastructures
(HalideIR and ISL schedule trees) turned into more impedance mismatch
problems than could be solved with a small tactical investment.
- Tensor Comprehensions emitted CUDA code which was then JIT compiled
with NVCC from a textual representation. While this was a pragmatic
short-term solution it made it hard to perform low-level rewrites that
would have helped with register reuse in the ***compute-bound regime***.
- The same reliance on emitting CUDA code made it difficult to
create cost models when time came. This made it artificially harder to
prune out bad solutions than necessary. This resulted in excessive
runtime evaluation, as reported in the paper [Machine Learning Systems
are Stuck in a Rut](https://dl.acm.org/doi/10.1145/3317550.3321441).
Many of those issues are naturally addressed by implementing these ideas
in the MLIR infrastructure.
### Lessons from Polyhedral compilers
The polyhedral model has been on the cutting edge of loop-level optimization for
decades, with several incarnations in production compilers such as
[GRAPHITE](https://gcc.gnu.org/wiki/Graphite) for GCC and
[Polly](https://polly.llvm.org) for LLVM. Although it has proved crucial to
generate efficient code from domain-specific languages such as
[PolyMage](http://mcl.csa.iisc.ac.in/polymage.html) and [Tensor
Comprehensions](https://dl.acm.org/doi/abs/10.1145/3355606), it has never been
fully included into mainstream general-purpose optimization pipelines. Detailed
analysis of the role of polyhedral transformations is provided in the
[simplified polyhedral
form](RationaleSimplifiedPolyhedralForm.md) document
dating back to the inception of MLIR.
In particular, polyhedral abstractions have proved challenging to integrate with
a more conventional compiler due to the following.
- The transformed code (or IR) quickly gets complex and thus hard to analyze and
understand.
- Code generation from the mathematical form used in the polyhedral model relies
on non-trivial exponentially complex algorithms.
- The mathematical form is rarely composable with the SSA representation and
related algorithms, on which most mainstream compilers are built today.
- Expressiveness limitations, although addressed in the scientific literature
through, e.g., summary functions, often remain present in actual
implementations.
The Affine dialect in MLIR was specifically designed to address the integration
problems mention above. In particular, it maintains the IR in the same form
(loops with additional constraints on how the bounds are expressed) throughout
the transformation, decreasing the need for one-shot conversion between
drastically different representations. It also embeds the polyhedral
representation into the SSA form by using MLIR regions and thus allows one to
combine polyhedral and SSA-based transformations.
### Lessons from the Affine dialect
The Affine dialect in MLIR brings the polyhedral abstraction closer to the
conventional SSA representation. It addresses several long-standing integration
challenges as described above and is likely to be more suitable when compiling
from a C language-level abstraction.
MLIR makes it possible to start from a higher-level abstraction than C, for
example in machine learning workloads. In such cases, it may be possible to
avoid complex analyses (data-flow analysis across loop iterations is
exponentially complex) required for polyhedral transformation by leveraging the
information available at higher levels of abstractions, similarly to DSL
compilers. Linalg intends to use this information when available and ensure
*legality of transformations by construction*, by integrating legality
preconditions in the op semantics (for example, loop tiling can be applied to
the loop nest computing a matrix multiplication, no need to additionally rely on
affine dependence analysis to check this). This information is not readily
available in the Affine dialect, and can only be derived using potentially
expensive pattern-matching algorithms.
Informed by the practical experience in polyhedral compilation and with the
Affine dialects in particular, Linalg takes the following decisions.
- **Discourage loop skewing**: the loop skewing transformation, that is
sometimes used to enable parallelization, often has surprising (negative)
effects on performance. In particular, polyhedral auto-transformation can be
expressed in a simpler way without loop skewing; skewing often leads to
complex control flow hampering performance on accelerators such as GPUs.
Moreover, the problems loop skewing addresses can be better addressed by other
approaches, e.g., diamond tiling. In the more restricted case of ML workloads,
multi-for loops with induction variables independent of each other (referred
to as hyper-rectangular iteration domains in the literature) such as the
proposed
[affine.parallel]((https://llvm.discourse.group/t/rfc-add-affine-parallel/350)
are sufficient in the majority of cases.
- **Declarative Tiling**: the *tiling* transformation is ubiquitous in HPC code
generation. It can be seen as a decomposition of either the iteration space or
the data space into smaller regular parts, referred to as tiles. Polyhedral
approaches, including the Affine dialect, mostly opt for iteration space
tiling, which introduces additional control flow and complex address
expressions. If the tile sizes are not known during the transformation (so
called parametric tiling), the address expressions and conditions quickly
become non-affine or require exponentially complex algorithms to reason about
them. Linalg focuses tiling on the data space instead, creating views into the
buffers that leverage MLIR's strided `memref` abstraction. These views compose
and the complexity of access expressions remains predictable.
- **Preserve high-level information**: Linalg maintains the information provided
by the op semantics as long as necessary for transformations. For example, the
result of tiling a matrix multiplication is loops around a smaller matrix
multiplication. Even with pattern-matching on top of the Affine dialect, this
would have required another step of pattern-matching after the transformation.
Given these choices, Linalg intends to be a better fit for **high-level
compilation** were significantly more information is readily available in the
input representation and should be leveraged before lowering to other
abstractions. Affine remains a strong abstraction for mid-level transformation
and is used as a lowering target for Linalg, enabling further transformations
and combination of semantically-loaded and lower-level inputs. As such, Linalg
is intended to complement Affine rather than replace it.
## Core Guiding Principles
### Transformations and Simplicity First
The purpose of the Linalg IR and its operations is primarily to:
- develop a set of key transformations, and
- make them correct by construction by carefully curating the set of
generic operation properties that drive applicability, and
- make them very simple to implement, apply, verify and especially
maintain.
The problem at hand is fundamentally driven by compilation of domain-specific
workloads for high-performance and parallel hardware architectures: **this is
an HPC compilation problem**.
The selection of relevant transformations follows a co-design approach and
involves considerations related to:
- concrete current and future needs of the application domain,
- concrete current and future hardware properties and ISAs,
- understanding of strengths and limitations of [existing approaches](#prior_art),
- taking advantage of the coexistence of multiple levels of IR in MLIR,
One needs to be methodical to avoid proliferation and redundancy. A given
transformation could exist at multiple levels of abstraction but **just
because one can write transformation X at level Y absolutely does not mean
one should**. This is where evaluation of existing
systems and acknowledgement of their strengths and weaknesses is crucial:
simplicity and maintainability aspects must be first-order concerns. Without
this additional effort of introspection, a design will not stand the test of
time. At the same time, complexity is very hard to ward off. It seems one needs
to suffer complexity to be prompted to take a step back and rethink
abstractions.
This is not merely a reimplementation of idea X in system Y: simplicity
**must be the outcome** of this introspection effort.
### Preservation of Information
The last two decades have seen a proliferation of Domain-Specific Languages
(DSLs) that have been very successful at limited application domains.
The main commonality between these systems is their use of a significantly
richer structural information than CFGs or loops.
Still, another commonality of existing systems is to lower to LLVM very quickly,
and cross a wide abstraction gap in a single step. This process often drops
semantic information that later needs to be reconstructed later,
when it is not irremediably lost.
These remarks, coupled with MLIR's suitability for defining IR at multiple
levels of abstraction led to the following 2 principles.
#### Declarative Specification: Avoid Raising
Compiler transformations need static structural information (e.g. loop-nests,
graphs of basic blocks, pure functions, etc). When that structural information
is lost, it needs to be reconstructed.
A good illustration of this phenomenon is the notion of *raising* in polyhedral
compilers: multiple polyhedral tools start by raising from a simplified C
form or from SSA IR into a higher-level representation that is more amenable
to loop transformations.
In advanced polyhedral compilers, a second type of raising
may typically exist to detect particular patterns (often variations of
BLAS). Such patterns may be broken by transformations making their detection
very fragile or even just impossible (incorrect).
MLIR makes it easy to define op semantics declaratively thanks to the use of
regions and attributes. This is an ideal opportunity to define new abstractions
to convey user-intent directly into the proper abstraction.
#### Progressive Lowering: Don't Lose Information too Quickly
Lowering too quickly to affine, generic loops or CFG form reduces the
amount of structure available to derive transformations from. While
manipulating loops is a net gain compared to CFG form for a certain class of
transformations, important information is still lost (e.g. parallel loops, or
mapping of a loop nest to an external implementation).
This creates non-trivial phase ordering issues. For instance, loop fusion may
easily destroy the ability to detect a BLAS pattern. One possible alternative
is to perform loop fusion, tiling, intra-tile loop distribution and then hope to
detect the BLAS pattern. Such a scheme presents difficult phase-ordering
constraints that will likely interfere with other decisions and passes.
Instead, certain Linalg ops are designed to maintain high-level information
across transformations such as tiling and fusion.
MLIR is designed as an infrastructure for ***progressive lowering***.
Linalg fully embraces this notion and thinks of codegen in terms of
*reducing a potential function*. That potential function is loosely
defined in terms of number of low-level instructions in a particular
Linalg ops (i.e. how heavy or lightweight the Linalg op is).
Linalg-based codegen and transformations start from higher-level IR
ops and dialects. Then each transformation application reduces the
potential by introducing lower-level IR ops and *smaller* Linalg ops.
This gradually reduces the potential, all the way to Loops + VectorOps
and LLVMIR.
### Composable and Declarative Transformations
Complex and impactful transformations need not be hard to manipulate, write or
maintain. Mixing XLA-style high-level op semantics knowledge with generic
properties to describe these semantics, directly in MLIR, is a promising way to:
- Design transformations that are correct by construction, easy to
write, easy to verify and easy to maintain.
- Provide a way to specify transformations and the units of IR they manipulate
declaratively. In turn this allows using local pattern rewrite rules in MLIR
(i.e. [DRR](../DeclarativeRewrites.md)).
- Allow creating customizable passes declaratively by simply selecting rewrite
rules. This allows mixing transformations, canonicalizations, constant folding
and other enabling rewrites in a single pass. The result is a system where pass
fusion is very simple to obtain and gives hope for solving certain
[phase ordering issues](https://dl.acm.org/doi/10.1145/201059.201061).
### Suitability for Search and Machine Learning
Compiler heuristics are hand-crafted human-engineered features: it is
ripe for disruption by machine-learning techniques.
To enable search, compiler transformations should be fine-grained,
[composable](#declarative_transformations) and expose tuning parameters that
can modify their behavior, guided by lessons from previous experience
with [Tensor Comprehensions](#lessonstc).
Of course, we are not advocating for using ML everywhere in the stack
immediately: low-level compilation and machine models are still quite performant
in LLVM. However, for the high-level and mid-level optimization problems,
models need to be conditioned (probabilistically) on the low-level
compiler which acts as a blackbox. For these reasons we prioritize the
design of IR and transformations with search-friendly properties over
building cost models.
Still, this does not mean Linalg refuses cost models: instead we
prefer to invest in infrastructure that will enable [ML-based
techniques to automatically build cost
models](http://homepages.inf.ed.ac.uk/hleather/publications/2009_autofeatures_cgo.pdf).
### Extensibility and Future-Proofness
MLIR allows defining IR for structured control flow and structured
data types. We choose to take advantage of these properties for the
reasons described above.
In particular, the `MemRefType` represents dense non-contiguous memory regions.
This structure should extend beyond simple dense data types and generalize to
ragged, sparse and mixed dens/sparse tensors as well as to trees, hash tables,
tables of records and maybe even graphs.
For such more advanced data types, the control-flow required to traverse the
data structures, termination conditions, etc are much less simple to analyze and
characterize statically. As a consequence we need to also design solutions that
stand a chance of evolving into runtime-adaptive computations (e.g.
inspector-executor in which an *inspector* runs a cheap runtime
analysis on the data to configure how the *executor* should run).
While there is no concrete solution
today to solve these problems in MLIR, it is pretty clear that perfect
static knowledge and analyses will not be serious contenders for these problems.
## Key Observations
The following key observations have influenced the design of Linalg and helped
reconcile [core guiding principles](#guiding_principles) with real-world
requirements when producing an implementation based on MLIR.
### Algorithms + Data Structures = Programs
This is a twist on Niklaus Wirth's formulation but captures the essence of the
design of Linalg: control-flow does not exist in a vacuum, independently of
data.
On the contrary, there is a very strong relationship between control-flow and
data structures: one cannot exist without the other. This has multiple
implications on the [semantics of Linalg Ops](#linalg_ops) and their
transformations. In particular, this observation influences whether
certain transformations are better done:
- as control flow or data structure manipulation,
- on Linalg ops attributes or on loops after some partial lowering
occurred,
- as extensions to the Linalg dialect in terms of new ops or attributes.
### The Dialect Need not be Closed Under Transformations
This is probably the most surprising and counter-intuitive
observation. When one designs IR for transformations, closed-ness is
often a non-negotiable property.
This is a key design principle of polyhedral IRs such as
[URUK](http://icps.u-strasbg.fr/~bastoul/research/papers/GVBCPST06-IJPP.pdf)
and
[ISL-based IRs](https://en.wikipedia.org/wiki/Integer_set_library):
they are closed under affine transformations.
In MLIR, multiple dialects coexist and form a coherent whole. After
experimenting with different alternatives, it became clear that strict
dialect closed-ness wasn't necessary and could be relaxed. Previous
systems did not have simple and principled means of building new IR
and probably suffered from this limitation. We conjecture this is a
key reason they required the IR to be closed under transformations.
Despite the fact that Linalg ops only allow perfectly nested
semantics, once tiling and fusion kick in, imperfectly nested loops
are gradually introduced.
In other words, imperfectly nested control flow appears as ***the result of
applying key transformations***.
Considering the *potential* described during the discussion on
[Progressive Lowering](#progressive_lowering), closed-ness under
transformation would dictate that the potential remains constant.
In contrast, Linalg advocates for ***monotonicity*** under
transformations.
### Summary of Existing Alternatives a Picture
Lastly, we summarize our observations of lessons from [Prior
Art](#prior_art)---when viewed under the lense of our [Core Guiding
Principles](#guiding_principles)---with the following picture.
The compilation flow combines [Halide](#lessonshalide) and a Polyhedral Compiler
derived from [ISL](https://en.wikipedia.org/wiki/Integer_set_library)
and uses both HalideIR and the ISL *schedule-tree* IR.
The compiler provides a collection of polyhedral compilation
algorithms to perform fusion and favor multi-level parallelism and
promotion to deeper levels of the memory hierarchy.
Tensor Comprehensions showed that, fixing a few predefined strategies
with parametric transformations and tuning knobs, can already provide
great results. In that previous work, simple
genetic search combined with an autotuning framework was sufficient
to find good implementations in the ***non-compute bound regime***.
This requires code versions obtainable by the
various transformations to encompass versions that get close to the
roofline limit.
The ultimate goal of Tensor Comprehensions was to concretely mix
Halide high-level transformations with polyhedral mid-level
transformations and build a pragmatic system that could take advantage
of both styles of compilation.
Linalg hopes to additionally address the following:
- Halide was never properly used in Tensor Comprehensions beyond shape
inference. Most of the investment went into simplifying polyhedral
transformations and building a usable end-to-end system. MLIR was
deemed a better infrastructure to mix these types of compilation.
- The early gains provided by reusing established infrastructures
(HalideIR and ISL schedule trees) turned into more impedance mismatch
problems than could be solved with a small tactical investment.
- Tensor Comprehensions emitted CUDA code which was then JIT compiled
with NVCC from a textual representation. While this was a pragmatic
short-term solution it made it hard to perform low-level rewrites that
would have helped with register reuse in the ***compute-bound regime***.
- The same reliance on emitting CUDA code made it difficult to
create cost models when time came. This made it artificially harder to
prune out bad solutions than necessary. This resulted in excessive
runtime evaluation, as reported in the paper [Machine Learning Systems
are Stuck in a Rut](https://dl.acm.org/doi/10.1145/3317550.3321441).
Many of those issues are naturally addressed by implementing these ideas
in the MLIR infrastructure.
### Lessons from Polyhedral compilers
The polyhedral model has been on the cutting edge of loop-level optimization for
decades, with several incarnations in production compilers such as
[GRAPHITE](https://gcc.gnu.org/wiki/Graphite) for GCC and
[Polly](https://polly.llvm.org) for LLVM. Although it has proved crucial to
generate efficient code from domain-specific languages such as
[PolyMage](http://mcl.csa.iisc.ac.in/polymage.html) and [Tensor
Comprehensions](https://dl.acm.org/doi/abs/10.1145/3355606), it has never been
fully included into mainstream general-purpose optimization pipelines. Detailed
analysis of the role of polyhedral transformations is provided in the
[simplified polyhedral
form](RationaleSimplifiedPolyhedralForm.md) document
dating back to the inception of MLIR.
In particular, polyhedral abstractions have proved challenging to integrate with
a more conventional compiler due to the following.
- The transformed code (or IR) quickly gets complex and thus hard to analyze and
understand.
- Code generation from the mathematical form used in the polyhedral model relies
on non-trivial exponentially complex algorithms.
- The mathematical form is rarely composable with the SSA representation and
related algorithms, on which most mainstream compilers are built today.
- Expressiveness limitations, although addressed in the scientific literature
through, e.g., summary functions, often remain present in actual
implementations.
The Affine dialect in MLIR was specifically designed to address the integration
problems mention above. In particular, it maintains the IR in the same form
(loops with additional constraints on how the bounds are expressed) throughout
the transformation, decreasing the need for one-shot conversion between
drastically different representations. It also embeds the polyhedral
representation into the SSA form by using MLIR regions and thus allows one to
combine polyhedral and SSA-based transformations.
### Lessons from the Affine dialect
The Affine dialect in MLIR brings the polyhedral abstraction closer to the
conventional SSA representation. It addresses several long-standing integration
challenges as described above and is likely to be more suitable when compiling
from a C language-level abstraction.
MLIR makes it possible to start from a higher-level abstraction than C, for
example in machine learning workloads. In such cases, it may be possible to
avoid complex analyses (data-flow analysis across loop iterations is
exponentially complex) required for polyhedral transformation by leveraging the
information available at higher levels of abstractions, similarly to DSL
compilers. Linalg intends to use this information when available and ensure
*legality of transformations by construction*, by integrating legality
preconditions in the op semantics (for example, loop tiling can be applied to
the loop nest computing a matrix multiplication, no need to additionally rely on
affine dependence analysis to check this). This information is not readily
available in the Affine dialect, and can only be derived using potentially
expensive pattern-matching algorithms.
Informed by the practical experience in polyhedral compilation and with the
Affine dialects in particular, Linalg takes the following decisions.
- **Discourage loop skewing**: the loop skewing transformation, that is
sometimes used to enable parallelization, often has surprising (negative)
effects on performance. In particular, polyhedral auto-transformation can be
expressed in a simpler way without loop skewing; skewing often leads to
complex control flow hampering performance on accelerators such as GPUs.
Moreover, the problems loop skewing addresses can be better addressed by other
approaches, e.g., diamond tiling. In the more restricted case of ML workloads,
multi-for loops with induction variables independent of each other (referred
to as hyper-rectangular iteration domains in the literature) such as the
proposed
[affine.parallel]((https://llvm.discourse.group/t/rfc-add-affine-parallel/350)
are sufficient in the majority of cases.
- **Declarative Tiling**: the *tiling* transformation is ubiquitous in HPC code
generation. It can be seen as a decomposition of either the iteration space or
the data space into smaller regular parts, referred to as tiles. Polyhedral
approaches, including the Affine dialect, mostly opt for iteration space
tiling, which introduces additional control flow and complex address
expressions. If the tile sizes are not known during the transformation (so
called parametric tiling), the address expressions and conditions quickly
become non-affine or require exponentially complex algorithms to reason about
them. Linalg focuses tiling on the data space instead, creating views into the
buffers that leverage MLIR's strided `memref` abstraction. These views compose
and the complexity of access expressions remains predictable.
- **Preserve high-level information**: Linalg maintains the information provided
by the op semantics as long as necessary for transformations. For example, the
result of tiling a matrix multiplication is loops around a smaller matrix
multiplication. Even with pattern-matching on top of the Affine dialect, this
would have required another step of pattern-matching after the transformation.
Given these choices, Linalg intends to be a better fit for **high-level
compilation** were significantly more information is readily available in the
input representation and should be leveraged before lowering to other
abstractions. Affine remains a strong abstraction for mid-level transformation
and is used as a lowering target for Linalg, enabling further transformations
and combination of semantically-loaded and lower-level inputs. As such, Linalg
is intended to complement Affine rather than replace it.
## Core Guiding Principles
### Transformations and Simplicity First
The purpose of the Linalg IR and its operations is primarily to:
- develop a set of key transformations, and
- make them correct by construction by carefully curating the set of
generic operation properties that drive applicability, and
- make them very simple to implement, apply, verify and especially
maintain.
The problem at hand is fundamentally driven by compilation of domain-specific
workloads for high-performance and parallel hardware architectures: **this is
an HPC compilation problem**.
The selection of relevant transformations follows a co-design approach and
involves considerations related to:
- concrete current and future needs of the application domain,
- concrete current and future hardware properties and ISAs,
- understanding of strengths and limitations of [existing approaches](#prior_art),
- taking advantage of the coexistence of multiple levels of IR in MLIR,
One needs to be methodical to avoid proliferation and redundancy. A given
transformation could exist at multiple levels of abstraction but **just
because one can write transformation X at level Y absolutely does not mean
one should**. This is where evaluation of existing
systems and acknowledgement of their strengths and weaknesses is crucial:
simplicity and maintainability aspects must be first-order concerns. Without
this additional effort of introspection, a design will not stand the test of
time. At the same time, complexity is very hard to ward off. It seems one needs
to suffer complexity to be prompted to take a step back and rethink
abstractions.
This is not merely a reimplementation of idea X in system Y: simplicity
**must be the outcome** of this introspection effort.
### Preservation of Information
The last two decades have seen a proliferation of Domain-Specific Languages
(DSLs) that have been very successful at limited application domains.
The main commonality between these systems is their use of a significantly
richer structural information than CFGs or loops.
Still, another commonality of existing systems is to lower to LLVM very quickly,
and cross a wide abstraction gap in a single step. This process often drops
semantic information that later needs to be reconstructed later,
when it is not irremediably lost.
These remarks, coupled with MLIR's suitability for defining IR at multiple
levels of abstraction led to the following 2 principles.
#### Declarative Specification: Avoid Raising
Compiler transformations need static structural information (e.g. loop-nests,
graphs of basic blocks, pure functions, etc). When that structural information
is lost, it needs to be reconstructed.
A good illustration of this phenomenon is the notion of *raising* in polyhedral
compilers: multiple polyhedral tools start by raising from a simplified C
form or from SSA IR into a higher-level representation that is more amenable
to loop transformations.
In advanced polyhedral compilers, a second type of raising
may typically exist to detect particular patterns (often variations of
BLAS). Such patterns may be broken by transformations making their detection
very fragile or even just impossible (incorrect).
MLIR makes it easy to define op semantics declaratively thanks to the use of
regions and attributes. This is an ideal opportunity to define new abstractions
to convey user-intent directly into the proper abstraction.
#### Progressive Lowering: Don't Lose Information too Quickly
Lowering too quickly to affine, generic loops or CFG form reduces the
amount of structure available to derive transformations from. While
manipulating loops is a net gain compared to CFG form for a certain class of
transformations, important information is still lost (e.g. parallel loops, or
mapping of a loop nest to an external implementation).
This creates non-trivial phase ordering issues. For instance, loop fusion may
easily destroy the ability to detect a BLAS pattern. One possible alternative
is to perform loop fusion, tiling, intra-tile loop distribution and then hope to
detect the BLAS pattern. Such a scheme presents difficult phase-ordering
constraints that will likely interfere with other decisions and passes.
Instead, certain Linalg ops are designed to maintain high-level information
across transformations such as tiling and fusion.
MLIR is designed as an infrastructure for ***progressive lowering***.
Linalg fully embraces this notion and thinks of codegen in terms of
*reducing a potential function*. That potential function is loosely
defined in terms of number of low-level instructions in a particular
Linalg ops (i.e. how heavy or lightweight the Linalg op is).
Linalg-based codegen and transformations start from higher-level IR
ops and dialects. Then each transformation application reduces the
potential by introducing lower-level IR ops and *smaller* Linalg ops.
This gradually reduces the potential, all the way to Loops + VectorOps
and LLVMIR.
### Composable and Declarative Transformations
Complex and impactful transformations need not be hard to manipulate, write or
maintain. Mixing XLA-style high-level op semantics knowledge with generic
properties to describe these semantics, directly in MLIR, is a promising way to:
- Design transformations that are correct by construction, easy to
write, easy to verify and easy to maintain.
- Provide a way to specify transformations and the units of IR they manipulate
declaratively. In turn this allows using local pattern rewrite rules in MLIR
(i.e. [DRR](../DeclarativeRewrites.md)).
- Allow creating customizable passes declaratively by simply selecting rewrite
rules. This allows mixing transformations, canonicalizations, constant folding
and other enabling rewrites in a single pass. The result is a system where pass
fusion is very simple to obtain and gives hope for solving certain
[phase ordering issues](https://dl.acm.org/doi/10.1145/201059.201061).
### Suitability for Search and Machine Learning
Compiler heuristics are hand-crafted human-engineered features: it is
ripe for disruption by machine-learning techniques.
To enable search, compiler transformations should be fine-grained,
[composable](#declarative_transformations) and expose tuning parameters that
can modify their behavior, guided by lessons from previous experience
with [Tensor Comprehensions](#lessonstc).
Of course, we are not advocating for using ML everywhere in the stack
immediately: low-level compilation and machine models are still quite performant
in LLVM. However, for the high-level and mid-level optimization problems,
models need to be conditioned (probabilistically) on the low-level
compiler which acts as a blackbox. For these reasons we prioritize the
design of IR and transformations with search-friendly properties over
building cost models.
Still, this does not mean Linalg refuses cost models: instead we
prefer to invest in infrastructure that will enable [ML-based
techniques to automatically build cost
models](http://homepages.inf.ed.ac.uk/hleather/publications/2009_autofeatures_cgo.pdf).
### Extensibility and Future-Proofness
MLIR allows defining IR for structured control flow and structured
data types. We choose to take advantage of these properties for the
reasons described above.
In particular, the `MemRefType` represents dense non-contiguous memory regions.
This structure should extend beyond simple dense data types and generalize to
ragged, sparse and mixed dens/sparse tensors as well as to trees, hash tables,
tables of records and maybe even graphs.
For such more advanced data types, the control-flow required to traverse the
data structures, termination conditions, etc are much less simple to analyze and
characterize statically. As a consequence we need to also design solutions that
stand a chance of evolving into runtime-adaptive computations (e.g.
inspector-executor in which an *inspector* runs a cheap runtime
analysis on the data to configure how the *executor* should run).
While there is no concrete solution
today to solve these problems in MLIR, it is pretty clear that perfect
static knowledge and analyses will not be serious contenders for these problems.
## Key Observations
The following key observations have influenced the design of Linalg and helped
reconcile [core guiding principles](#guiding_principles) with real-world
requirements when producing an implementation based on MLIR.
### Algorithms + Data Structures = Programs
This is a twist on Niklaus Wirth's formulation but captures the essence of the
design of Linalg: control-flow does not exist in a vacuum, independently of
data.
On the contrary, there is a very strong relationship between control-flow and
data structures: one cannot exist without the other. This has multiple
implications on the [semantics of Linalg Ops](#linalg_ops) and their
transformations. In particular, this observation influences whether
certain transformations are better done:
- as control flow or data structure manipulation,
- on Linalg ops attributes or on loops after some partial lowering
occurred,
- as extensions to the Linalg dialect in terms of new ops or attributes.
### The Dialect Need not be Closed Under Transformations
This is probably the most surprising and counter-intuitive
observation. When one designs IR for transformations, closed-ness is
often a non-negotiable property.
This is a key design principle of polyhedral IRs such as
[URUK](http://icps.u-strasbg.fr/~bastoul/research/papers/GVBCPST06-IJPP.pdf)
and
[ISL-based IRs](https://en.wikipedia.org/wiki/Integer_set_library):
they are closed under affine transformations.
In MLIR, multiple dialects coexist and form a coherent whole. After
experimenting with different alternatives, it became clear that strict
dialect closed-ness wasn't necessary and could be relaxed. Previous
systems did not have simple and principled means of building new IR
and probably suffered from this limitation. We conjecture this is a
key reason they required the IR to be closed under transformations.
Despite the fact that Linalg ops only allow perfectly nested
semantics, once tiling and fusion kick in, imperfectly nested loops
are gradually introduced.
In other words, imperfectly nested control flow appears as ***the result of
applying key transformations***.
Considering the *potential* described during the discussion on
[Progressive Lowering](#progressive_lowering), closed-ness under
transformation would dictate that the potential remains constant.
In contrast, Linalg advocates for ***monotonicity*** under
transformations.
### Summary of Existing Alternatives a Picture
Lastly, we summarize our observations of lessons from [Prior
Art](#prior_art)---when viewed under the lense of our [Core Guiding
Principles](#guiding_principles)---with the following picture.
 This figure is not meant to be perfectly accurate but a rough map of
how we view the distribution of structural information in existing
systems, from a codegen-friendly angle. Unsurprisingly, the
[Linalg Dialect](../Dialects/Linalg/) and its
future evolutions aspire to a position in the top-right of this map.
This figure is not meant to be perfectly accurate but a rough map of
how we view the distribution of structural information in existing
systems, from a codegen-friendly angle. Unsurprisingly, the
[Linalg Dialect](../Dialects/Linalg/) and its
future evolutions aspire to a position in the top-right of this map.
 This document describes the key design principles
that led to the existing implementation of Linalg and aims at exposing
the tradeoffs involved when building higher-level Intermediate
Representations (IR) and Dialects to facilitate code
generation. Consider the simplified schema describing codegen in MLIR.
Linalg is designed to solve the High-level Hierarchical Optimization
(HHO box) and to interoperate nicely within a
*Mixture Of Expert Compilers* environment (i.e. the *CGSel* box).
This work is inspired by a wealth of [prior art](#prior_art) in
the field, from which it seeks to learn key lessons. This documentation
and introspection effort also comes in the context of the proposal for a
working group for discussing the [Development of high-level Tensor Compute
Primitives dialect(s) and
transformations](https://llvm.discourse.group/t/development-of-high-level-tensor-compute-primitives-dialect-s-and-transformations/388/3).
We hope that the lessons from prior art, the design principles outlined in
this doc and the architecture of Linalg can help inform the community on a
path to defining these High-Level Tensor Compute Primitives.
### Inception
Linalg started as a pragmatic dialect to bootstrap code generation in MLIR, by
*defining away* complex code generation problems like precise dependence
analysis or polyhedral code generation and by introducing the ability to call
into fast library implementations when available. Linalg **defines ops and
transformations declaratively** and was originally restricted to ops with
*linear-algebra like* semantics (`pointwise`, `matmul`, `conv`...). This
approach enables building a high-level productivity-first codegen solution that
leverages *both* compiler optimizations *and* efficient library implementations
so as not to miss out on simple performance benefits. For example, if
one's favorite HPC library or ISA has a `matmul` primitive running at 95% of
the achievable peak performance, for operands stored in some memory, one should
be able to **use the primitive** when possible *and* generate code otherwise.
However, as the design of Linalg co-evolved with the design of MLIR, it became
apparent that it could extend to larger application domains than just machine
learning on dense tensors.
The design and evolution of Linalg follow a *codegen-friendly* approach where
the IR and the transformations evolve hand-in-hand.
The key idea is that op semantics *declare* and transport information that is
traditionally obtained by compiler analyses.
This information captures the legality and applicability of transformations and
is **not lost by lowering prematurely to loop or CFG form**. The key
transformations are designed so as to **preserve this information** as long as
necessary. For example, `linalg.matmul` remains `linalg.matmul` after tiling
and fusion.
Furthermore, Linalg decouples transformation validity from profitability
considerations and voluntarily leaves the latter aside in the first iteration
(see the [suitability for search](#suitability_for_search) guiding principle).
The first incarnation of these ideas was presented as an example at the
EuroLLVM 2019 developer's meeting as part of the
[Linalg section](https://llvm.org/devmtg/2019-04/slides/Tutorial-AminiVasilacheZinenko-MLIR.pdf)
of the first [MLIR Tutorial](https://www.youtube.com/watch?v=cyICUIZ56wQ).
### Evolution
Since the initial implementation, the design has evolved with, and partially
driven the evolution of the core MLIR infrastructure to use
[Regions](https://mlir.llvm.org/docs/LangRef/#regions),
[OpInterfaces](https://mlir.llvm.org/docs/Interfaces/),
[ODS](https://mlir.llvm.org/docs/OpDefinitions/) and
[Declarative Rewrite Rules](https://mlir.llvm.org/docs/DeclarativeRewrites/)
among others. The approach adopted by Linalg was extended to become
[StructuredOps abstractions](
https://drive.google.com/drive/u/0/folders/1sRAsgsd8Bvpm_IxREmZf2agsGU2KvrK-),
with Linalg becoming its incarnation on tensors and buffers.
It is complemented by the
[Vector dialect](https://mlir.llvm.org/docs/Dialects/Vector/),
which defines structured operations on vectors, following the same rationale and
design principles as Linalg. (Vector dialect includes the higher-level
operations on multi-dimensional vectors and abstracts away the lowering to
single-dimensional vectors).
The Linalg dialect itself grew beyond linear algebra-like operations to become
more expressive, in particular by providing an abstraction of a loop nest
supporting parallelism, reductions and sliding windows around arbitrary MLIR
[regions](https://mlir.llvm.org/docs/LangRef/#regions). It also has the
potential of growing beyond *dense* linear-algebra to support richer data
types, such as sparse and ragged tensors and buffers.
Linalg design remains open to evolution and cross-pollination with other
dialects and approaches. It has been successfully used as the staging ground
for code generation-related abstractions, spinning off the generalization of
the following:
- the `!linalg.view` type folded into the *"Strided MemRef"* type while
preserving structure to allow calling into external C++ libraries with
unsurprising ABI conventions;
- the `linalg.view` and `linalg.subview` ops evolved into the standard dialect;
- the `linalg.for`, `linalg.load` and `linalg.store` ops evolved into a prelude
to the *structured control flow* dialect (named `LoopOps`).
More components can be extracted, redesigned and generalized when new uses or
requirements arise.
Several [design questions](#open_issues) remain open in Linalg, which does not
claim to be a general solution to all compilation problems.
It does aim at driving thinking and implementations of domain-specific
abstractions where programmer's intent can be captured at a very high level,
directly in the IR.
Given the evolution of the scope, it becomes apparent that a better name than
"Linalg" could remove some of the confusions related to the dialect (and the
underlying approach), its goals and limitations.
## Prior Art
Linalg draws inspiration from decades of prior art to design a modern a
pragmatic solution. The following non-exhaustive list refers to some of the
projects that influenced Linalg design:
- [ONNX](https://onnx.ai/),
- [LIFT](https://www.lift-project.org/),
- [XLA](https://www.tensorflow.org/xla/architecture),
- [Halide](https://halide-lang.org/) and [TVM](https://tvm.apache.org/),
- [TACO](http://tensor-compiler.org/),
- [Darkroom](http://darkroom-lang.org/) and [Terra](http://terralang.org/),
- [Sigma-LL](http://spiral.ece.cmu.edu:8080/pub-spiral/pubfile/cgo16-preprint_248.pdf),
- [Tensor Comprehensions](https://arxiv.org/abs/1802.04730),
- [Polyhedral Compilers](https://en.wikipedia.org/wiki/Polytope_model),
- the [Affine dialect](https://mlir.llvm.org/docs/Dialects/Affine/) in MLIR,
- Generic Loop Transformations (see Ken Kennedy's
[Optimizing Compilers for Modern Architectures](
https://www.elsevier.com/books/optimizing-compilers-for-modern-architectures/allen/978-0-08-051324-9))
- Traditional compiler CFGs with SSA forms.
Additionally, experience with the following tools proved very valuable when
thinking holistically about how all these components interplay all the way
up to the user and down to the hardware:
- the [Torch](http://torch.ch/) machine-learning framework,
- the LLVM compiler, specifically in JIT mode,
- high-performance libraries (MKL, CUBLAS, FBFFT)
- the [PeachPy](https://www.cs.utexas.edu/users/flame/BLISRetreat/BLISRetreatTalks/PeachPy.pdf) assembler
- current and potentially upcoming hardware ISAs.
The novelty of MLIR's code base and its unprecedented support for defining and
mixing abstractions, enabling one to reflect on and integrate the key elements
of the prior art success as well as avoid the common pitfalls in the area of
code generation. Thus, instead of diverging into a discussion about the
implications of adopting any of the existing solutions, Linalg had the
possibility to build on all of them and learn from their experience while
leveraging the benefit of hindsight.
The following reflections on prior art have influenced the design of Linalg.
The discussion is by no means exhaustive but should capture the key motivations
behind Linalg.
### Lessons from ONNX
ONNX is a specification of operations that appear in Machine Learning
workloads. As such, it is predominantly driven by the expressiveness requirements
of ML, and less by the considerations of IR design for HPC code generation.
Similarly to ONNX, Linalg defines *"semantically charged" named ops*.
But it also considers *transformations on these ops* as a key component and
defines the IR to support the transformations, preferring transformations over
expressiveness if necessary.
Linalg hopes to additionally address the following:
- facilitate frontend-compiler co-design by taking into account compiler
transformations and lowerings in op definition;
- minimize the set of available ops by making them non-overlapping with each
other, thus simplifying the intermediate representation.
### Lessons from LIFT
[LIFT](https://www.lift-project.org/) is a system to write computational
kernels based on functional abstractions. Transformations are
represented by additional nodes in the IR, whose semantics are at the
level of the algorithm (e.g. `partialReduce`).
LIFT applies and composes transformations by using [local rewrite
rules](https://www.lift-project.org/presentations/2015/ICFP-2015.pdf) that
embed these additional nodes directly in the functional abstraction.
Similarly to LIFT, Linalg uses local rewrite rules implemented with the MLIR
[Declarative Rewrite Rules](https://mlir.llvm.org/docs/DeclarativeRewrites/)
mechanisms.
Linalg builds on, and helps separate concerns in the LIFT approach as follows:
- transformations are either separated from the representation or expressed as
composable attributes that are independent of the actual computation,
avoiding intricate effects on performance;
- abstractions are split into smaller components (e.g., control flow and data
structure abstractions) potentially reusable across different dialects in the
MLIR's open ecosystem.
LIFT is expected to further influence the design of Linalg as it evolves. In
particular, extending the data structure abstractions to support non-dense
tensors can use the experience of LIFT abstractions for
[sparse](https://www.lift-project.org/publications/2016/harries16sparse.pdf)
and [position-dependent
arrays](https://www.lift-project.org/publications/2019/pizzuti19positiondependentarrays.pdf).
### Lessons from XLA
[XLA](https://www.tensorflow.org/xla/architecture) is one of the first
post-Theano ML compilers that was introduced as a pragmatic compilation
solution for TensorFlow. It shines on Google's xPU
hardware and is an important piece of the puzzle. It is particularly good at
(1) transforming code back and forth between the scalar and the vector
worlds, (2) passing function boundaries for handling both host and device
code, and (3) complying to stringent requirements imposed by energy-efficient
xPUs.
XLA followed a pragmatic design process where the compiler is given perfect
knowledge of each op's semantic, all starting from the mighty `conv` and
`matmul` ops. XLA transformations consist of writing emitters that compose, as C++
functions. Perfect op semantics knowledge has 2 big benefits: (1) transformations are
correct by construction (2) very strong performance on difficult xPU targets.
Similarly, Linalg ops *"know their semantics"* and *"know how to transform and
lower themselves"*. The means by which this information is made available and
how it is used in MLIR are, however, very different.
Linalg hopes to additionally address the following:
- HLOs are expressive as a whole, but each op has very limited and fixed
semantics: ops are not configurable. As a consequence, HLOs have evolved into
a too large set of ops whose semantics intersect.
This echoes the ops proliferation problem also exhibited by ONNX.
- Reliance on perfect op knowledge leads to situations where transformations and
ops end up needing to know about each other's semantics (e.g. during fusion).
Since the transformations themselves are not simple local rewrite patterns
(unlike LIFT), code complexity grows quickly.
- XLA lacks an independent IR that can be inspected, unit tested and used
independently. This monolithic design makes the system not portable: xPU passes
and GPU passes do not share much code.
### Lessons from Halide and TVM
[Halide](https://halide-lang.org/) is a DSL embedded in C++ that provides a
way of metaprogramming the HalideIR and applying transformations declaratively
to let the expert user transform and optimize the program in tailored ways.
Halide, initially targeted the SIGGRAPH community but is now more generally
applicable. [TVM](https://tvm.apache.org/) is an evolution of Halide into the
machine learning and deep-neural network space, based on HalideIR.
The Halide transformation methodology follows similar principles to the
[URUK](http://icps.u-strasbg.fr/~bastoul/research/papers/GVBCPST06-IJPP.pdf)
and
[CHiLL](https://pdfs.semanticscholar.org/6a46/20589f63f3385707d2d590f7b7dc8ee4d74f.pdf)
compiler transformation frameworks, but without the strengths (and especially
complexity) of the polyhedral model.
Halide particularly shines at making the HPC transformation methodology
accessible to $\Omega$(10-100) users, at a time when polyhedral tools are
still only accessible to $\Omega$(1-10) users. Halide makes heavy usage of
canonicalization rules that are also very prevalent in MLIR.
Linalg hopes to additionally address the following:
- Halide scheduling is powerful and explores a large swath of possible
transformations. But it's still too hard for newcomers to use or extend. The
level of performance you get from Halide is very different depending on
whether one is a seasoned veteran or a newcomer. This is especially true as
the number of transformations grows.
- Halide raises rather than lowers in two ways, going counter-current to the
design goals we set for high-level codegen abstractions in MLIR. First,
canonical Halide front-end code uses explicit indexing and math on scalar
values, so to target BLAS/DNN libraries one needs to add pattern matching
which is similarly brittle as in the affine case. While Halide's performance
is on par with the libraries on programmable targets (CPU/GPU), that
approach doesn't work on mobile accelerators or on xPUs, where the framework
ingests whole-tensor operations.
Second, reductions and scans are expressed using serial iteration, again
requiring pattern matching before they can be transformed (e.g. to do a
reduction using atomics, or hierarchically). The lesson to draw is that we
should start with higher-level primitives than Halide.
### Lessons from Tensor Comprehensions
[Tensor Comprehensions](https://arxiv.org/abs/1802.04730) is a
high-level language to express tensor computations with a syntax
generalizing the Einstein notation, coupled to an end-to-end
compilation flow capable of lowering to efficient GPU code. It was
integrated with 2 ML frameworks: Caffe2 and PyTorch.
This document describes the key design principles
that led to the existing implementation of Linalg and aims at exposing
the tradeoffs involved when building higher-level Intermediate
Representations (IR) and Dialects to facilitate code
generation. Consider the simplified schema describing codegen in MLIR.
Linalg is designed to solve the High-level Hierarchical Optimization
(HHO box) and to interoperate nicely within a
*Mixture Of Expert Compilers* environment (i.e. the *CGSel* box).
This work is inspired by a wealth of [prior art](#prior_art) in
the field, from which it seeks to learn key lessons. This documentation
and introspection effort also comes in the context of the proposal for a
working group for discussing the [Development of high-level Tensor Compute
Primitives dialect(s) and
transformations](https://llvm.discourse.group/t/development-of-high-level-tensor-compute-primitives-dialect-s-and-transformations/388/3).
We hope that the lessons from prior art, the design principles outlined in
this doc and the architecture of Linalg can help inform the community on a
path to defining these High-Level Tensor Compute Primitives.
### Inception
Linalg started as a pragmatic dialect to bootstrap code generation in MLIR, by
*defining away* complex code generation problems like precise dependence
analysis or polyhedral code generation and by introducing the ability to call
into fast library implementations when available. Linalg **defines ops and
transformations declaratively** and was originally restricted to ops with
*linear-algebra like* semantics (`pointwise`, `matmul`, `conv`...). This
approach enables building a high-level productivity-first codegen solution that
leverages *both* compiler optimizations *and* efficient library implementations
so as not to miss out on simple performance benefits. For example, if
one's favorite HPC library or ISA has a `matmul` primitive running at 95% of
the achievable peak performance, for operands stored in some memory, one should
be able to **use the primitive** when possible *and* generate code otherwise.
However, as the design of Linalg co-evolved with the design of MLIR, it became
apparent that it could extend to larger application domains than just machine
learning on dense tensors.
The design and evolution of Linalg follow a *codegen-friendly* approach where
the IR and the transformations evolve hand-in-hand.
The key idea is that op semantics *declare* and transport information that is
traditionally obtained by compiler analyses.
This information captures the legality and applicability of transformations and
is **not lost by lowering prematurely to loop or CFG form**. The key
transformations are designed so as to **preserve this information** as long as
necessary. For example, `linalg.matmul` remains `linalg.matmul` after tiling
and fusion.
Furthermore, Linalg decouples transformation validity from profitability
considerations and voluntarily leaves the latter aside in the first iteration
(see the [suitability for search](#suitability_for_search) guiding principle).
The first incarnation of these ideas was presented as an example at the
EuroLLVM 2019 developer's meeting as part of the
[Linalg section](https://llvm.org/devmtg/2019-04/slides/Tutorial-AminiVasilacheZinenko-MLIR.pdf)
of the first [MLIR Tutorial](https://www.youtube.com/watch?v=cyICUIZ56wQ).
### Evolution
Since the initial implementation, the design has evolved with, and partially
driven the evolution of the core MLIR infrastructure to use
[Regions](https://mlir.llvm.org/docs/LangRef/#regions),
[OpInterfaces](https://mlir.llvm.org/docs/Interfaces/),
[ODS](https://mlir.llvm.org/docs/OpDefinitions/) and
[Declarative Rewrite Rules](https://mlir.llvm.org/docs/DeclarativeRewrites/)
among others. The approach adopted by Linalg was extended to become
[StructuredOps abstractions](
https://drive.google.com/drive/u/0/folders/1sRAsgsd8Bvpm_IxREmZf2agsGU2KvrK-),
with Linalg becoming its incarnation on tensors and buffers.
It is complemented by the
[Vector dialect](https://mlir.llvm.org/docs/Dialects/Vector/),
which defines structured operations on vectors, following the same rationale and
design principles as Linalg. (Vector dialect includes the higher-level
operations on multi-dimensional vectors and abstracts away the lowering to
single-dimensional vectors).
The Linalg dialect itself grew beyond linear algebra-like operations to become
more expressive, in particular by providing an abstraction of a loop nest
supporting parallelism, reductions and sliding windows around arbitrary MLIR
[regions](https://mlir.llvm.org/docs/LangRef/#regions). It also has the
potential of growing beyond *dense* linear-algebra to support richer data
types, such as sparse and ragged tensors and buffers.
Linalg design remains open to evolution and cross-pollination with other
dialects and approaches. It has been successfully used as the staging ground
for code generation-related abstractions, spinning off the generalization of
the following:
- the `!linalg.view` type folded into the *"Strided MemRef"* type while
preserving structure to allow calling into external C++ libraries with
unsurprising ABI conventions;
- the `linalg.view` and `linalg.subview` ops evolved into the standard dialect;
- the `linalg.for`, `linalg.load` and `linalg.store` ops evolved into a prelude
to the *structured control flow* dialect (named `LoopOps`).
More components can be extracted, redesigned and generalized when new uses or
requirements arise.
Several [design questions](#open_issues) remain open in Linalg, which does not
claim to be a general solution to all compilation problems.
It does aim at driving thinking and implementations of domain-specific
abstractions where programmer's intent can be captured at a very high level,
directly in the IR.
Given the evolution of the scope, it becomes apparent that a better name than
"Linalg" could remove some of the confusions related to the dialect (and the
underlying approach), its goals and limitations.
## Prior Art
Linalg draws inspiration from decades of prior art to design a modern a
pragmatic solution. The following non-exhaustive list refers to some of the
projects that influenced Linalg design:
- [ONNX](https://onnx.ai/),
- [LIFT](https://www.lift-project.org/),
- [XLA](https://www.tensorflow.org/xla/architecture),
- [Halide](https://halide-lang.org/) and [TVM](https://tvm.apache.org/),
- [TACO](http://tensor-compiler.org/),
- [Darkroom](http://darkroom-lang.org/) and [Terra](http://terralang.org/),
- [Sigma-LL](http://spiral.ece.cmu.edu:8080/pub-spiral/pubfile/cgo16-preprint_248.pdf),
- [Tensor Comprehensions](https://arxiv.org/abs/1802.04730),
- [Polyhedral Compilers](https://en.wikipedia.org/wiki/Polytope_model),
- the [Affine dialect](https://mlir.llvm.org/docs/Dialects/Affine/) in MLIR,
- Generic Loop Transformations (see Ken Kennedy's
[Optimizing Compilers for Modern Architectures](
https://www.elsevier.com/books/optimizing-compilers-for-modern-architectures/allen/978-0-08-051324-9))
- Traditional compiler CFGs with SSA forms.
Additionally, experience with the following tools proved very valuable when
thinking holistically about how all these components interplay all the way
up to the user and down to the hardware:
- the [Torch](http://torch.ch/) machine-learning framework,
- the LLVM compiler, specifically in JIT mode,
- high-performance libraries (MKL, CUBLAS, FBFFT)
- the [PeachPy](https://www.cs.utexas.edu/users/flame/BLISRetreat/BLISRetreatTalks/PeachPy.pdf) assembler
- current and potentially upcoming hardware ISAs.
The novelty of MLIR's code base and its unprecedented support for defining and
mixing abstractions, enabling one to reflect on and integrate the key elements
of the prior art success as well as avoid the common pitfalls in the area of
code generation. Thus, instead of diverging into a discussion about the
implications of adopting any of the existing solutions, Linalg had the
possibility to build on all of them and learn from their experience while
leveraging the benefit of hindsight.
The following reflections on prior art have influenced the design of Linalg.
The discussion is by no means exhaustive but should capture the key motivations
behind Linalg.
### Lessons from ONNX
ONNX is a specification of operations that appear in Machine Learning
workloads. As such, it is predominantly driven by the expressiveness requirements
of ML, and less by the considerations of IR design for HPC code generation.
Similarly to ONNX, Linalg defines *"semantically charged" named ops*.
But it also considers *transformations on these ops* as a key component and
defines the IR to support the transformations, preferring transformations over
expressiveness if necessary.
Linalg hopes to additionally address the following:
- facilitate frontend-compiler co-design by taking into account compiler
transformations and lowerings in op definition;
- minimize the set of available ops by making them non-overlapping with each
other, thus simplifying the intermediate representation.
### Lessons from LIFT
[LIFT](https://www.lift-project.org/) is a system to write computational
kernels based on functional abstractions. Transformations are
represented by additional nodes in the IR, whose semantics are at the
level of the algorithm (e.g. `partialReduce`).
LIFT applies and composes transformations by using [local rewrite
rules](https://www.lift-project.org/presentations/2015/ICFP-2015.pdf) that
embed these additional nodes directly in the functional abstraction.
Similarly to LIFT, Linalg uses local rewrite rules implemented with the MLIR
[Declarative Rewrite Rules](https://mlir.llvm.org/docs/DeclarativeRewrites/)
mechanisms.
Linalg builds on, and helps separate concerns in the LIFT approach as follows:
- transformations are either separated from the representation or expressed as
composable attributes that are independent of the actual computation,
avoiding intricate effects on performance;
- abstractions are split into smaller components (e.g., control flow and data
structure abstractions) potentially reusable across different dialects in the
MLIR's open ecosystem.
LIFT is expected to further influence the design of Linalg as it evolves. In
particular, extending the data structure abstractions to support non-dense
tensors can use the experience of LIFT abstractions for
[sparse](https://www.lift-project.org/publications/2016/harries16sparse.pdf)
and [position-dependent
arrays](https://www.lift-project.org/publications/2019/pizzuti19positiondependentarrays.pdf).
### Lessons from XLA
[XLA](https://www.tensorflow.org/xla/architecture) is one of the first
post-Theano ML compilers that was introduced as a pragmatic compilation
solution for TensorFlow. It shines on Google's xPU
hardware and is an important piece of the puzzle. It is particularly good at
(1) transforming code back and forth between the scalar and the vector
worlds, (2) passing function boundaries for handling both host and device
code, and (3) complying to stringent requirements imposed by energy-efficient
xPUs.
XLA followed a pragmatic design process where the compiler is given perfect
knowledge of each op's semantic, all starting from the mighty `conv` and
`matmul` ops. XLA transformations consist of writing emitters that compose, as C++
functions. Perfect op semantics knowledge has 2 big benefits: (1) transformations are
correct by construction (2) very strong performance on difficult xPU targets.
Similarly, Linalg ops *"know their semantics"* and *"know how to transform and
lower themselves"*. The means by which this information is made available and
how it is used in MLIR are, however, very different.
Linalg hopes to additionally address the following:
- HLOs are expressive as a whole, but each op has very limited and fixed
semantics: ops are not configurable. As a consequence, HLOs have evolved into
a too large set of ops whose semantics intersect.
This echoes the ops proliferation problem also exhibited by ONNX.
- Reliance on perfect op knowledge leads to situations where transformations and
ops end up needing to know about each other's semantics (e.g. during fusion).
Since the transformations themselves are not simple local rewrite patterns
(unlike LIFT), code complexity grows quickly.
- XLA lacks an independent IR that can be inspected, unit tested and used
independently. This monolithic design makes the system not portable: xPU passes
and GPU passes do not share much code.
### Lessons from Halide and TVM
[Halide](https://halide-lang.org/) is a DSL embedded in C++ that provides a
way of metaprogramming the HalideIR and applying transformations declaratively
to let the expert user transform and optimize the program in tailored ways.
Halide, initially targeted the SIGGRAPH community but is now more generally
applicable. [TVM](https://tvm.apache.org/) is an evolution of Halide into the
machine learning and deep-neural network space, based on HalideIR.
The Halide transformation methodology follows similar principles to the
[URUK](http://icps.u-strasbg.fr/~bastoul/research/papers/GVBCPST06-IJPP.pdf)
and
[CHiLL](https://pdfs.semanticscholar.org/6a46/20589f63f3385707d2d590f7b7dc8ee4d74f.pdf)
compiler transformation frameworks, but without the strengths (and especially
complexity) of the polyhedral model.
Halide particularly shines at making the HPC transformation methodology
accessible to $\Omega$(10-100) users, at a time when polyhedral tools are
still only accessible to $\Omega$(1-10) users. Halide makes heavy usage of
canonicalization rules that are also very prevalent in MLIR.
Linalg hopes to additionally address the following:
- Halide scheduling is powerful and explores a large swath of possible
transformations. But it's still too hard for newcomers to use or extend. The
level of performance you get from Halide is very different depending on
whether one is a seasoned veteran or a newcomer. This is especially true as
the number of transformations grows.
- Halide raises rather than lowers in two ways, going counter-current to the
design goals we set for high-level codegen abstractions in MLIR. First,
canonical Halide front-end code uses explicit indexing and math on scalar
values, so to target BLAS/DNN libraries one needs to add pattern matching
which is similarly brittle as in the affine case. While Halide's performance
is on par with the libraries on programmable targets (CPU/GPU), that
approach doesn't work on mobile accelerators or on xPUs, where the framework
ingests whole-tensor operations.
Second, reductions and scans are expressed using serial iteration, again
requiring pattern matching before they can be transformed (e.g. to do a
reduction using atomics, or hierarchically). The lesson to draw is that we
should start with higher-level primitives than Halide.
### Lessons from Tensor Comprehensions
[Tensor Comprehensions](https://arxiv.org/abs/1802.04730) is a
high-level language to express tensor computations with a syntax
generalizing the Einstein notation, coupled to an end-to-end
compilation flow capable of lowering to efficient GPU code. It was
integrated with 2 ML frameworks: Caffe2 and PyTorch.
 The compilation flow combines [Halide](#lessonshalide) and a Polyhedral Compiler
derived from [ISL](https://en.wikipedia.org/wiki/Integer_set_library)
and uses both HalideIR and the ISL *schedule-tree* IR.
The compiler provides a collection of polyhedral compilation
algorithms to perform fusion and favor multi-level parallelism and
promotion to deeper levels of the memory hierarchy.
Tensor Comprehensions showed that, fixing a few predefined strategies
with parametric transformations and tuning knobs, can already provide
great results. In that previous work, simple
genetic search combined with an autotuning framework was sufficient
to find good implementations in the ***non-compute bound regime***.
This requires code versions obtainable by the
various transformations to encompass versions that get close to the
roofline limit.
The ultimate goal of Tensor Comprehensions was to concretely mix
Halide high-level transformations with polyhedral mid-level
transformations and build a pragmatic system that could take advantage
of both styles of compilation.
Linalg hopes to additionally address the following:
- Halide was never properly used in Tensor Comprehensions beyond shape
inference. Most of the investment went into simplifying polyhedral
transformations and building a usable end-to-end system. MLIR was
deemed a better infrastructure to mix these types of compilation.
- The early gains provided by reusing established infrastructures
(HalideIR and ISL schedule trees) turned into more impedance mismatch
problems than could be solved with a small tactical investment.
- Tensor Comprehensions emitted CUDA code which was then JIT compiled
with NVCC from a textual representation. While this was a pragmatic
short-term solution it made it hard to perform low-level rewrites that
would have helped with register reuse in the ***compute-bound regime***.
- The same reliance on emitting CUDA code made it difficult to
create cost models when time came. This made it artificially harder to
prune out bad solutions than necessary. This resulted in excessive
runtime evaluation, as reported in the paper [Machine Learning Systems
are Stuck in a Rut](https://dl.acm.org/doi/10.1145/3317550.3321441).
Many of those issues are naturally addressed by implementing these ideas
in the MLIR infrastructure.
### Lessons from Polyhedral compilers
The polyhedral model has been on the cutting edge of loop-level optimization for
decades, with several incarnations in production compilers such as
[GRAPHITE](https://gcc.gnu.org/wiki/Graphite) for GCC and
[Polly](https://polly.llvm.org) for LLVM. Although it has proved crucial to
generate efficient code from domain-specific languages such as
[PolyMage](http://mcl.csa.iisc.ac.in/polymage.html) and [Tensor
Comprehensions](https://dl.acm.org/doi/abs/10.1145/3355606), it has never been
fully included into mainstream general-purpose optimization pipelines. Detailed
analysis of the role of polyhedral transformations is provided in the
[simplified polyhedral
form](RationaleSimplifiedPolyhedralForm.md) document
dating back to the inception of MLIR.
In particular, polyhedral abstractions have proved challenging to integrate with
a more conventional compiler due to the following.
- The transformed code (or IR) quickly gets complex and thus hard to analyze and
understand.
- Code generation from the mathematical form used in the polyhedral model relies
on non-trivial exponentially complex algorithms.
- The mathematical form is rarely composable with the SSA representation and
related algorithms, on which most mainstream compilers are built today.
- Expressiveness limitations, although addressed in the scientific literature
through, e.g., summary functions, often remain present in actual
implementations.
The Affine dialect in MLIR was specifically designed to address the integration
problems mention above. In particular, it maintains the IR in the same form
(loops with additional constraints on how the bounds are expressed) throughout
the transformation, decreasing the need for one-shot conversion between
drastically different representations. It also embeds the polyhedral
representation into the SSA form by using MLIR regions and thus allows one to
combine polyhedral and SSA-based transformations.
### Lessons from the Affine dialect
The Affine dialect in MLIR brings the polyhedral abstraction closer to the
conventional SSA representation. It addresses several long-standing integration
challenges as described above and is likely to be more suitable when compiling
from a C language-level abstraction.
MLIR makes it possible to start from a higher-level abstraction than C, for
example in machine learning workloads. In such cases, it may be possible to
avoid complex analyses (data-flow analysis across loop iterations is
exponentially complex) required for polyhedral transformation by leveraging the
information available at higher levels of abstractions, similarly to DSL
compilers. Linalg intends to use this information when available and ensure
*legality of transformations by construction*, by integrating legality
preconditions in the op semantics (for example, loop tiling can be applied to
the loop nest computing a matrix multiplication, no need to additionally rely on
affine dependence analysis to check this). This information is not readily
available in the Affine dialect, and can only be derived using potentially
expensive pattern-matching algorithms.
Informed by the practical experience in polyhedral compilation and with the
Affine dialects in particular, Linalg takes the following decisions.
- **Discourage loop skewing**: the loop skewing transformation, that is
sometimes used to enable parallelization, often has surprising (negative)
effects on performance. In particular, polyhedral auto-transformation can be
expressed in a simpler way without loop skewing; skewing often leads to
complex control flow hampering performance on accelerators such as GPUs.
Moreover, the problems loop skewing addresses can be better addressed by other
approaches, e.g., diamond tiling. In the more restricted case of ML workloads,
multi-for loops with induction variables independent of each other (referred
to as hyper-rectangular iteration domains in the literature) such as the
proposed
[affine.parallel]((https://llvm.discourse.group/t/rfc-add-affine-parallel/350)
are sufficient in the majority of cases.
- **Declarative Tiling**: the *tiling* transformation is ubiquitous in HPC code
generation. It can be seen as a decomposition of either the iteration space or
the data space into smaller regular parts, referred to as tiles. Polyhedral
approaches, including the Affine dialect, mostly opt for iteration space
tiling, which introduces additional control flow and complex address
expressions. If the tile sizes are not known during the transformation (so
called parametric tiling), the address expressions and conditions quickly
become non-affine or require exponentially complex algorithms to reason about
them. Linalg focuses tiling on the data space instead, creating views into the
buffers that leverage MLIR's strided `memref` abstraction. These views compose
and the complexity of access expressions remains predictable.
- **Preserve high-level information**: Linalg maintains the information provided
by the op semantics as long as necessary for transformations. For example, the
result of tiling a matrix multiplication is loops around a smaller matrix
multiplication. Even with pattern-matching on top of the Affine dialect, this
would have required another step of pattern-matching after the transformation.
Given these choices, Linalg intends to be a better fit for **high-level
compilation** were significantly more information is readily available in the
input representation and should be leveraged before lowering to other
abstractions. Affine remains a strong abstraction for mid-level transformation
and is used as a lowering target for Linalg, enabling further transformations
and combination of semantically-loaded and lower-level inputs. As such, Linalg
is intended to complement Affine rather than replace it.
## Core Guiding Principles
### Transformations and Simplicity First
The purpose of the Linalg IR and its operations is primarily to:
- develop a set of key transformations, and
- make them correct by construction by carefully curating the set of
generic operation properties that drive applicability, and
- make them very simple to implement, apply, verify and especially
maintain.
The problem at hand is fundamentally driven by compilation of domain-specific
workloads for high-performance and parallel hardware architectures: **this is
an HPC compilation problem**.
The selection of relevant transformations follows a co-design approach and
involves considerations related to:
- concrete current and future needs of the application domain,
- concrete current and future hardware properties and ISAs,
- understanding of strengths and limitations of [existing approaches](#prior_art),
- taking advantage of the coexistence of multiple levels of IR in MLIR,
One needs to be methodical to avoid proliferation and redundancy. A given
transformation could exist at multiple levels of abstraction but **just
because one can write transformation X at level Y absolutely does not mean
one should**. This is where evaluation of existing
systems and acknowledgement of their strengths and weaknesses is crucial:
simplicity and maintainability aspects must be first-order concerns. Without
this additional effort of introspection, a design will not stand the test of
time. At the same time, complexity is very hard to ward off. It seems one needs
to suffer complexity to be prompted to take a step back and rethink
abstractions.
This is not merely a reimplementation of idea X in system Y: simplicity
**must be the outcome** of this introspection effort.
### Preservation of Information
The last two decades have seen a proliferation of Domain-Specific Languages
(DSLs) that have been very successful at limited application domains.
The main commonality between these systems is their use of a significantly
richer structural information than CFGs or loops.
Still, another commonality of existing systems is to lower to LLVM very quickly,
and cross a wide abstraction gap in a single step. This process often drops
semantic information that later needs to be reconstructed later,
when it is not irremediably lost.
These remarks, coupled with MLIR's suitability for defining IR at multiple
levels of abstraction led to the following 2 principles.
#### Declarative Specification: Avoid Raising
Compiler transformations need static structural information (e.g. loop-nests,
graphs of basic blocks, pure functions, etc). When that structural information
is lost, it needs to be reconstructed.
A good illustration of this phenomenon is the notion of *raising* in polyhedral
compilers: multiple polyhedral tools start by raising from a simplified C
form or from SSA IR into a higher-level representation that is more amenable
to loop transformations.
In advanced polyhedral compilers, a second type of raising
may typically exist to detect particular patterns (often variations of
BLAS). Such patterns may be broken by transformations making their detection
very fragile or even just impossible (incorrect).
MLIR makes it easy to define op semantics declaratively thanks to the use of
regions and attributes. This is an ideal opportunity to define new abstractions
to convey user-intent directly into the proper abstraction.
#### Progressive Lowering: Don't Lose Information too Quickly
Lowering too quickly to affine, generic loops or CFG form reduces the
amount of structure available to derive transformations from. While
manipulating loops is a net gain compared to CFG form for a certain class of
transformations, important information is still lost (e.g. parallel loops, or
mapping of a loop nest to an external implementation).
This creates non-trivial phase ordering issues. For instance, loop fusion may
easily destroy the ability to detect a BLAS pattern. One possible alternative
is to perform loop fusion, tiling, intra-tile loop distribution and then hope to
detect the BLAS pattern. Such a scheme presents difficult phase-ordering
constraints that will likely interfere with other decisions and passes.
Instead, certain Linalg ops are designed to maintain high-level information
across transformations such as tiling and fusion.
MLIR is designed as an infrastructure for ***progressive lowering***.
Linalg fully embraces this notion and thinks of codegen in terms of
*reducing a potential function*. That potential function is loosely
defined in terms of number of low-level instructions in a particular
Linalg ops (i.e. how heavy or lightweight the Linalg op is).
Linalg-based codegen and transformations start from higher-level IR
ops and dialects. Then each transformation application reduces the
potential by introducing lower-level IR ops and *smaller* Linalg ops.
This gradually reduces the potential, all the way to Loops + VectorOps
and LLVMIR.
### Composable and Declarative Transformations
Complex and impactful transformations need not be hard to manipulate, write or
maintain. Mixing XLA-style high-level op semantics knowledge with generic
properties to describe these semantics, directly in MLIR, is a promising way to:
- Design transformations that are correct by construction, easy to
write, easy to verify and easy to maintain.
- Provide a way to specify transformations and the units of IR they manipulate
declaratively. In turn this allows using local pattern rewrite rules in MLIR
(i.e. [DRR](../DeclarativeRewrites.md)).
- Allow creating customizable passes declaratively by simply selecting rewrite
rules. This allows mixing transformations, canonicalizations, constant folding
and other enabling rewrites in a single pass. The result is a system where pass
fusion is very simple to obtain and gives hope for solving certain
[phase ordering issues](https://dl.acm.org/doi/10.1145/201059.201061).
### Suitability for Search and Machine Learning
Compiler heuristics are hand-crafted human-engineered features: it is
ripe for disruption by machine-learning techniques.
To enable search, compiler transformations should be fine-grained,
[composable](#declarative_transformations) and expose tuning parameters that
can modify their behavior, guided by lessons from previous experience
with [Tensor Comprehensions](#lessonstc).
Of course, we are not advocating for using ML everywhere in the stack
immediately: low-level compilation and machine models are still quite performant
in LLVM. However, for the high-level and mid-level optimization problems,
models need to be conditioned (probabilistically) on the low-level
compiler which acts as a blackbox. For these reasons we prioritize the
design of IR and transformations with search-friendly properties over
building cost models.
Still, this does not mean Linalg refuses cost models: instead we
prefer to invest in infrastructure that will enable [ML-based
techniques to automatically build cost
models](http://homepages.inf.ed.ac.uk/hleather/publications/2009_autofeatures_cgo.pdf).
### Extensibility and Future-Proofness
MLIR allows defining IR for structured control flow and structured
data types. We choose to take advantage of these properties for the
reasons described above.
In particular, the `MemRefType` represents dense non-contiguous memory regions.
This structure should extend beyond simple dense data types and generalize to
ragged, sparse and mixed dens/sparse tensors as well as to trees, hash tables,
tables of records and maybe even graphs.
For such more advanced data types, the control-flow required to traverse the
data structures, termination conditions, etc are much less simple to analyze and
characterize statically. As a consequence we need to also design solutions that
stand a chance of evolving into runtime-adaptive computations (e.g.
inspector-executor in which an *inspector* runs a cheap runtime
analysis on the data to configure how the *executor* should run).
While there is no concrete solution
today to solve these problems in MLIR, it is pretty clear that perfect
static knowledge and analyses will not be serious contenders for these problems.
## Key Observations
The following key observations have influenced the design of Linalg and helped
reconcile [core guiding principles](#guiding_principles) with real-world
requirements when producing an implementation based on MLIR.
### Algorithms + Data Structures = Programs
This is a twist on Niklaus Wirth's formulation but captures the essence of the
design of Linalg: control-flow does not exist in a vacuum, independently of
data.
On the contrary, there is a very strong relationship between control-flow and
data structures: one cannot exist without the other. This has multiple
implications on the [semantics of Linalg Ops](#linalg_ops) and their
transformations. In particular, this observation influences whether
certain transformations are better done:
- as control flow or data structure manipulation,
- on Linalg ops attributes or on loops after some partial lowering
occurred,
- as extensions to the Linalg dialect in terms of new ops or attributes.
### The Dialect Need not be Closed Under Transformations
This is probably the most surprising and counter-intuitive
observation. When one designs IR for transformations, closed-ness is
often a non-negotiable property.
This is a key design principle of polyhedral IRs such as
[URUK](http://icps.u-strasbg.fr/~bastoul/research/papers/GVBCPST06-IJPP.pdf)
and
[ISL-based IRs](https://en.wikipedia.org/wiki/Integer_set_library):
they are closed under affine transformations.
In MLIR, multiple dialects coexist and form a coherent whole. After
experimenting with different alternatives, it became clear that strict
dialect closed-ness wasn't necessary and could be relaxed. Previous
systems did not have simple and principled means of building new IR
and probably suffered from this limitation. We conjecture this is a
key reason they required the IR to be closed under transformations.
Despite the fact that Linalg ops only allow perfectly nested
semantics, once tiling and fusion kick in, imperfectly nested loops
are gradually introduced.
In other words, imperfectly nested control flow appears as ***the result of
applying key transformations***.
Considering the *potential* described during the discussion on
[Progressive Lowering](#progressive_lowering), closed-ness under
transformation would dictate that the potential remains constant.
In contrast, Linalg advocates for ***monotonicity*** under
transformations.
### Summary of Existing Alternatives a Picture
Lastly, we summarize our observations of lessons from [Prior
Art](#prior_art)---when viewed under the lense of our [Core Guiding
Principles](#guiding_principles)---with the following picture.
The compilation flow combines [Halide](#lessonshalide) and a Polyhedral Compiler
derived from [ISL](https://en.wikipedia.org/wiki/Integer_set_library)
and uses both HalideIR and the ISL *schedule-tree* IR.
The compiler provides a collection of polyhedral compilation
algorithms to perform fusion and favor multi-level parallelism and
promotion to deeper levels of the memory hierarchy.
Tensor Comprehensions showed that, fixing a few predefined strategies
with parametric transformations and tuning knobs, can already provide
great results. In that previous work, simple
genetic search combined with an autotuning framework was sufficient
to find good implementations in the ***non-compute bound regime***.
This requires code versions obtainable by the
various transformations to encompass versions that get close to the
roofline limit.
The ultimate goal of Tensor Comprehensions was to concretely mix
Halide high-level transformations with polyhedral mid-level
transformations and build a pragmatic system that could take advantage
of both styles of compilation.
Linalg hopes to additionally address the following:
- Halide was never properly used in Tensor Comprehensions beyond shape
inference. Most of the investment went into simplifying polyhedral
transformations and building a usable end-to-end system. MLIR was
deemed a better infrastructure to mix these types of compilation.
- The early gains provided by reusing established infrastructures
(HalideIR and ISL schedule trees) turned into more impedance mismatch
problems than could be solved with a small tactical investment.
- Tensor Comprehensions emitted CUDA code which was then JIT compiled
with NVCC from a textual representation. While this was a pragmatic
short-term solution it made it hard to perform low-level rewrites that
would have helped with register reuse in the ***compute-bound regime***.
- The same reliance on emitting CUDA code made it difficult to
create cost models when time came. This made it artificially harder to
prune out bad solutions than necessary. This resulted in excessive
runtime evaluation, as reported in the paper [Machine Learning Systems
are Stuck in a Rut](https://dl.acm.org/doi/10.1145/3317550.3321441).
Many of those issues are naturally addressed by implementing these ideas
in the MLIR infrastructure.
### Lessons from Polyhedral compilers
The polyhedral model has been on the cutting edge of loop-level optimization for
decades, with several incarnations in production compilers such as
[GRAPHITE](https://gcc.gnu.org/wiki/Graphite) for GCC and
[Polly](https://polly.llvm.org) for LLVM. Although it has proved crucial to
generate efficient code from domain-specific languages such as
[PolyMage](http://mcl.csa.iisc.ac.in/polymage.html) and [Tensor
Comprehensions](https://dl.acm.org/doi/abs/10.1145/3355606), it has never been
fully included into mainstream general-purpose optimization pipelines. Detailed
analysis of the role of polyhedral transformations is provided in the
[simplified polyhedral
form](RationaleSimplifiedPolyhedralForm.md) document
dating back to the inception of MLIR.
In particular, polyhedral abstractions have proved challenging to integrate with
a more conventional compiler due to the following.
- The transformed code (or IR) quickly gets complex and thus hard to analyze and
understand.
- Code generation from the mathematical form used in the polyhedral model relies
on non-trivial exponentially complex algorithms.
- The mathematical form is rarely composable with the SSA representation and
related algorithms, on which most mainstream compilers are built today.
- Expressiveness limitations, although addressed in the scientific literature
through, e.g., summary functions, often remain present in actual
implementations.
The Affine dialect in MLIR was specifically designed to address the integration
problems mention above. In particular, it maintains the IR in the same form
(loops with additional constraints on how the bounds are expressed) throughout
the transformation, decreasing the need for one-shot conversion between
drastically different representations. It also embeds the polyhedral
representation into the SSA form by using MLIR regions and thus allows one to
combine polyhedral and SSA-based transformations.
### Lessons from the Affine dialect
The Affine dialect in MLIR brings the polyhedral abstraction closer to the
conventional SSA representation. It addresses several long-standing integration
challenges as described above and is likely to be more suitable when compiling
from a C language-level abstraction.
MLIR makes it possible to start from a higher-level abstraction than C, for
example in machine learning workloads. In such cases, it may be possible to
avoid complex analyses (data-flow analysis across loop iterations is
exponentially complex) required for polyhedral transformation by leveraging the
information available at higher levels of abstractions, similarly to DSL
compilers. Linalg intends to use this information when available and ensure
*legality of transformations by construction*, by integrating legality
preconditions in the op semantics (for example, loop tiling can be applied to
the loop nest computing a matrix multiplication, no need to additionally rely on
affine dependence analysis to check this). This information is not readily
available in the Affine dialect, and can only be derived using potentially
expensive pattern-matching algorithms.
Informed by the practical experience in polyhedral compilation and with the
Affine dialects in particular, Linalg takes the following decisions.
- **Discourage loop skewing**: the loop skewing transformation, that is
sometimes used to enable parallelization, often has surprising (negative)
effects on performance. In particular, polyhedral auto-transformation can be
expressed in a simpler way without loop skewing; skewing often leads to
complex control flow hampering performance on accelerators such as GPUs.
Moreover, the problems loop skewing addresses can be better addressed by other
approaches, e.g., diamond tiling. In the more restricted case of ML workloads,
multi-for loops with induction variables independent of each other (referred
to as hyper-rectangular iteration domains in the literature) such as the
proposed
[affine.parallel]((https://llvm.discourse.group/t/rfc-add-affine-parallel/350)
are sufficient in the majority of cases.
- **Declarative Tiling**: the *tiling* transformation is ubiquitous in HPC code
generation. It can be seen as a decomposition of either the iteration space or
the data space into smaller regular parts, referred to as tiles. Polyhedral
approaches, including the Affine dialect, mostly opt for iteration space
tiling, which introduces additional control flow and complex address
expressions. If the tile sizes are not known during the transformation (so
called parametric tiling), the address expressions and conditions quickly
become non-affine or require exponentially complex algorithms to reason about
them. Linalg focuses tiling on the data space instead, creating views into the
buffers that leverage MLIR's strided `memref` abstraction. These views compose
and the complexity of access expressions remains predictable.
- **Preserve high-level information**: Linalg maintains the information provided
by the op semantics as long as necessary for transformations. For example, the
result of tiling a matrix multiplication is loops around a smaller matrix
multiplication. Even with pattern-matching on top of the Affine dialect, this
would have required another step of pattern-matching after the transformation.
Given these choices, Linalg intends to be a better fit for **high-level
compilation** were significantly more information is readily available in the
input representation and should be leveraged before lowering to other
abstractions. Affine remains a strong abstraction for mid-level transformation
and is used as a lowering target for Linalg, enabling further transformations
and combination of semantically-loaded and lower-level inputs. As such, Linalg
is intended to complement Affine rather than replace it.
## Core Guiding Principles
### Transformations and Simplicity First
The purpose of the Linalg IR and its operations is primarily to:
- develop a set of key transformations, and
- make them correct by construction by carefully curating the set of
generic operation properties that drive applicability, and
- make them very simple to implement, apply, verify and especially
maintain.
The problem at hand is fundamentally driven by compilation of domain-specific
workloads for high-performance and parallel hardware architectures: **this is
an HPC compilation problem**.
The selection of relevant transformations follows a co-design approach and
involves considerations related to:
- concrete current and future needs of the application domain,
- concrete current and future hardware properties and ISAs,
- understanding of strengths and limitations of [existing approaches](#prior_art),
- taking advantage of the coexistence of multiple levels of IR in MLIR,
One needs to be methodical to avoid proliferation and redundancy. A given
transformation could exist at multiple levels of abstraction but **just
because one can write transformation X at level Y absolutely does not mean
one should**. This is where evaluation of existing
systems and acknowledgement of their strengths and weaknesses is crucial:
simplicity and maintainability aspects must be first-order concerns. Without
this additional effort of introspection, a design will not stand the test of
time. At the same time, complexity is very hard to ward off. It seems one needs
to suffer complexity to be prompted to take a step back and rethink
abstractions.
This is not merely a reimplementation of idea X in system Y: simplicity
**must be the outcome** of this introspection effort.
### Preservation of Information
The last two decades have seen a proliferation of Domain-Specific Languages
(DSLs) that have been very successful at limited application domains.
The main commonality between these systems is their use of a significantly
richer structural information than CFGs or loops.
Still, another commonality of existing systems is to lower to LLVM very quickly,
and cross a wide abstraction gap in a single step. This process often drops
semantic information that later needs to be reconstructed later,
when it is not irremediably lost.
These remarks, coupled with MLIR's suitability for defining IR at multiple
levels of abstraction led to the following 2 principles.
#### Declarative Specification: Avoid Raising
Compiler transformations need static structural information (e.g. loop-nests,
graphs of basic blocks, pure functions, etc). When that structural information
is lost, it needs to be reconstructed.
A good illustration of this phenomenon is the notion of *raising* in polyhedral
compilers: multiple polyhedral tools start by raising from a simplified C
form or from SSA IR into a higher-level representation that is more amenable
to loop transformations.
In advanced polyhedral compilers, a second type of raising
may typically exist to detect particular patterns (often variations of
BLAS). Such patterns may be broken by transformations making their detection
very fragile or even just impossible (incorrect).
MLIR makes it easy to define op semantics declaratively thanks to the use of
regions and attributes. This is an ideal opportunity to define new abstractions
to convey user-intent directly into the proper abstraction.
#### Progressive Lowering: Don't Lose Information too Quickly
Lowering too quickly to affine, generic loops or CFG form reduces the
amount of structure available to derive transformations from. While
manipulating loops is a net gain compared to CFG form for a certain class of
transformations, important information is still lost (e.g. parallel loops, or
mapping of a loop nest to an external implementation).
This creates non-trivial phase ordering issues. For instance, loop fusion may
easily destroy the ability to detect a BLAS pattern. One possible alternative
is to perform loop fusion, tiling, intra-tile loop distribution and then hope to
detect the BLAS pattern. Such a scheme presents difficult phase-ordering
constraints that will likely interfere with other decisions and passes.
Instead, certain Linalg ops are designed to maintain high-level information
across transformations such as tiling and fusion.
MLIR is designed as an infrastructure for ***progressive lowering***.
Linalg fully embraces this notion and thinks of codegen in terms of
*reducing a potential function*. That potential function is loosely
defined in terms of number of low-level instructions in a particular
Linalg ops (i.e. how heavy or lightweight the Linalg op is).
Linalg-based codegen and transformations start from higher-level IR
ops and dialects. Then each transformation application reduces the
potential by introducing lower-level IR ops and *smaller* Linalg ops.
This gradually reduces the potential, all the way to Loops + VectorOps
and LLVMIR.
### Composable and Declarative Transformations
Complex and impactful transformations need not be hard to manipulate, write or
maintain. Mixing XLA-style high-level op semantics knowledge with generic
properties to describe these semantics, directly in MLIR, is a promising way to:
- Design transformations that are correct by construction, easy to
write, easy to verify and easy to maintain.
- Provide a way to specify transformations and the units of IR they manipulate
declaratively. In turn this allows using local pattern rewrite rules in MLIR
(i.e. [DRR](../DeclarativeRewrites.md)).
- Allow creating customizable passes declaratively by simply selecting rewrite
rules. This allows mixing transformations, canonicalizations, constant folding
and other enabling rewrites in a single pass. The result is a system where pass
fusion is very simple to obtain and gives hope for solving certain
[phase ordering issues](https://dl.acm.org/doi/10.1145/201059.201061).
### Suitability for Search and Machine Learning
Compiler heuristics are hand-crafted human-engineered features: it is
ripe for disruption by machine-learning techniques.
To enable search, compiler transformations should be fine-grained,
[composable](#declarative_transformations) and expose tuning parameters that
can modify their behavior, guided by lessons from previous experience
with [Tensor Comprehensions](#lessonstc).
Of course, we are not advocating for using ML everywhere in the stack
immediately: low-level compilation and machine models are still quite performant
in LLVM. However, for the high-level and mid-level optimization problems,
models need to be conditioned (probabilistically) on the low-level
compiler which acts as a blackbox. For these reasons we prioritize the
design of IR and transformations with search-friendly properties over
building cost models.
Still, this does not mean Linalg refuses cost models: instead we
prefer to invest in infrastructure that will enable [ML-based
techniques to automatically build cost
models](http://homepages.inf.ed.ac.uk/hleather/publications/2009_autofeatures_cgo.pdf).
### Extensibility and Future-Proofness
MLIR allows defining IR for structured control flow and structured
data types. We choose to take advantage of these properties for the
reasons described above.
In particular, the `MemRefType` represents dense non-contiguous memory regions.
This structure should extend beyond simple dense data types and generalize to
ragged, sparse and mixed dens/sparse tensors as well as to trees, hash tables,
tables of records and maybe even graphs.
For such more advanced data types, the control-flow required to traverse the
data structures, termination conditions, etc are much less simple to analyze and
characterize statically. As a consequence we need to also design solutions that
stand a chance of evolving into runtime-adaptive computations (e.g.
inspector-executor in which an *inspector* runs a cheap runtime
analysis on the data to configure how the *executor* should run).
While there is no concrete solution
today to solve these problems in MLIR, it is pretty clear that perfect
static knowledge and analyses will not be serious contenders for these problems.
## Key Observations
The following key observations have influenced the design of Linalg and helped
reconcile [core guiding principles](#guiding_principles) with real-world
requirements when producing an implementation based on MLIR.
### Algorithms + Data Structures = Programs
This is a twist on Niklaus Wirth's formulation but captures the essence of the
design of Linalg: control-flow does not exist in a vacuum, independently of
data.
On the contrary, there is a very strong relationship between control-flow and
data structures: one cannot exist without the other. This has multiple
implications on the [semantics of Linalg Ops](#linalg_ops) and their
transformations. In particular, this observation influences whether
certain transformations are better done:
- as control flow or data structure manipulation,
- on Linalg ops attributes or on loops after some partial lowering
occurred,
- as extensions to the Linalg dialect in terms of new ops or attributes.
### The Dialect Need not be Closed Under Transformations
This is probably the most surprising and counter-intuitive
observation. When one designs IR for transformations, closed-ness is
often a non-negotiable property.
This is a key design principle of polyhedral IRs such as
[URUK](http://icps.u-strasbg.fr/~bastoul/research/papers/GVBCPST06-IJPP.pdf)
and
[ISL-based IRs](https://en.wikipedia.org/wiki/Integer_set_library):
they are closed under affine transformations.
In MLIR, multiple dialects coexist and form a coherent whole. After
experimenting with different alternatives, it became clear that strict
dialect closed-ness wasn't necessary and could be relaxed. Previous
systems did not have simple and principled means of building new IR
and probably suffered from this limitation. We conjecture this is a
key reason they required the IR to be closed under transformations.
Despite the fact that Linalg ops only allow perfectly nested
semantics, once tiling and fusion kick in, imperfectly nested loops
are gradually introduced.
In other words, imperfectly nested control flow appears as ***the result of
applying key transformations***.
Considering the *potential* described during the discussion on
[Progressive Lowering](#progressive_lowering), closed-ness under
transformation would dictate that the potential remains constant.
In contrast, Linalg advocates for ***monotonicity*** under
transformations.
### Summary of Existing Alternatives a Picture
Lastly, we summarize our observations of lessons from [Prior
Art](#prior_art)---when viewed under the lense of our [Core Guiding
Principles](#guiding_principles)---with the following picture.
 This figure is not meant to be perfectly accurate but a rough map of
how we view the distribution of structural information in existing
systems, from a codegen-friendly angle. Unsurprisingly, the
[Linalg Dialect](../Dialects/Linalg/) and its
future evolutions aspire to a position in the top-right of this map.
This figure is not meant to be perfectly accurate but a rough map of
how we view the distribution of structural information in existing
systems, from a codegen-friendly angle. Unsurprisingly, the
[Linalg Dialect](../Dialects/Linalg/) and its
future evolutions aspire to a position in the top-right of this map.